
如图,正方形卡片A类,B类和长方形卡片C类若干张,如果要拼一个长为(a+2b),宽为(a+b)的大长方形,则需要C类卡片( )
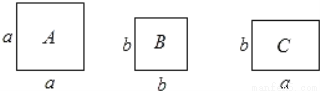
A. 2张 B. 3张 C. 4张 D. 5张
B 【解析】试题分析:(a+2b)(a+b)=a2+ab+2ab+2b2=a2+3ab+2b2, 则需要C类卡片张数为3. 故选B.科目:初中数学 来源:江苏省盐城市2017-2018学年八年级12月联合质量调研数学试卷 题型:解答题
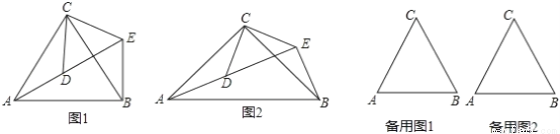
(1)问题发现:如图1,△ACB和△DCE均为等边三角形,当△DCE旋转至点A,D,E在同一直线上,连接BE.
填空:① ∠AEB的度数为_______;②线段AD、BE之间的数量关系是______.
(2)拓展研究:
如图2,△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=90°,点A、D、E在同一直线上,若AE=15,DE=7,求AB的长度.
(3)探究发现:
图1中的△ACB和△DCE,在△DCE旋转过程中当点A,D,E不在同一直线上时,设直线AD与BE相交于点O,试在备用图中探索∠AOE的度数,直接写出结果,不必说明理由.
【答案】(1)60°.AD=BE;(2)AB=17;(3)∠AOE的度数是60°或120°.
【解析】试题分析:(1)由条件易证△ACD≌△BCE,从而得到:AD=BE,∠ADC=∠BEC.由点A,D,E在同一直线上可求出∠ADC,从而可以求出∠AEB的度数.
(2)仿照(1)中的解法可求出∠AEB的度数,证出AD=BE;由△DCE为等腰直角三角形及CM为△DCE中DE边上的高可得CM=DM=ME,从而证到AE=2CH+BE.
(3)由(1)知△ACD≌△BCE,得∠CAD=∠CBE,由∠CAB=∠ABC=60°,可知∠EAB+∠ABE=120°,根据三角形的内角和定理可知∠AOE=60°.
试题解析:(1)①∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°.
∴∠ACD=∠BCE.
在△ACD和△BCE中,
 ,
,
∴△ACD≌△BCE(SAS).
∴∠ADC=∠BEC.
∵△DCE为等边三角形,
∴∠CDE=∠CED=60°.
∵点A,D,E在同一直线上,
∴∠ADC=120°.
∴∠BEC=120°.
∴∠AEB=∠BEC?∠CED=60°.
故答案为:60°.
②∵△ACD≌△BCE,
∴AD=BE.
故答案为:AD=BE.
(2)∵△ACB和△DCE均为等腰直角三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=90°.
∴∠ACD=∠BCE.
在△ACD和△BCE中,
 ,
,
∴△ACD≌△BCE(SAS).
∴AD=BE=AE-DE=8,∠ADC=∠BEC,
∵△DCE为等腰直角三角形,
∴∠CDE=∠CED=45°.
∵点A,D,E在同一直线上,
∴∠ADC=135°.
∴∠BEC=135°.
∴∠AEB=∠BEC?∠CED=90°.
∴AB=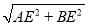 =17;
=17;
(3)由(1)知△ACD≌△BCE,
∴∠CAD=∠CBE,
∵∠CAB=∠CBA=60°,
∴∠OAB+∠OBA=120°
∴∠AOE=180°?120°=60°,
同理求得∠AOB=60°,
∴∠AOE=120°,
∴∠AOE的度数是60°或120°.
点睛:本题考查了等边三角形的性质、等腰三角形的性质、直角三角形斜边上的中线等于斜边的一半、三角形全等的判定与性质等知识,考查了运用已有的知识和经验解决问题的能力.
【题型】解答题
【结束】
26
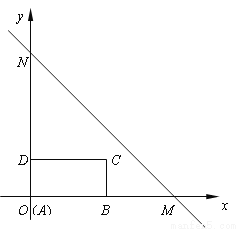
如图,直线MN:y=-x+b与x轴交于点M(4,0),与y轴交于点N,长方形ABCD的边AB在x轴上,AB=2,AD=1.长方形ABCD由点A与点O重合的位置开始,以每秒1个单位长度的速度沿x轴正方向作匀速直线运动,当点A与点M重合时停止运动.设长方形运动的时间为t秒,长方形ABCD与△OMN重合部分的面积为S.
(1)求直线MN的解析式;
(2)当t=1时,请判断点C是否在直线MN上,并说明理由;
(3)请求出当t为何值时,点D在直线MN上;
(4)直接写出在整个运动过程中S与t的函数关系式
查看答案和解析>>
科目:初中数学 来源:2016-2017学年陕西师大附中七年级(下)第一次月考数学试卷 题型:填空题
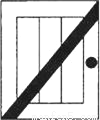
如图,为了使一扇旧木门不变形,木工师傅在木门的背后加钉了一根木条,这样做的道理是_____.
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市黄泥学校2016-2017学年上期八年级期中测评数学试卷 题型:解答题
因式分【解析】
(1)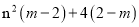 (2)
(2)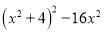 (3)
(3)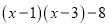
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市黄泥学校2016-2017学年上期八年级期中测评数学试卷 题型:填空题
计算: 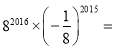 ________.
________.
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市黄泥学校2016-2017学年上期八年级期中测评数学试卷 题型:单选题
下列从左边到右边的变形,属于因式分解的是( )
A. 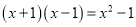 B.
B. 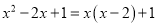
C. 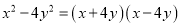 D.
D. 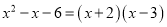
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市黄泥学校2016-2017学年上期八年级期中测评数学试卷 题型:单选题
4的平方根是( )
A. 2 B. -2 C. 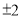 D.
D. 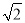
查看答案和解析>>
科目:初中数学 来源:重庆市江津区2016-2017学年八年级下学期期末考试数学试卷 题型:单选题
如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )
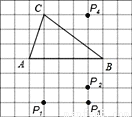
A. 1个 B. 2个 C. 3个 D. 4个
C 【解析】要使△ABP与△ABC全等,必须使点P到AB的距离等于点C到AB的距离,即3个单位长度,所以点P的位置可以是P1,P3,P4三个,故选C.查看答案和解析>>
科目:初中数学 来源:2017年广东省河源市中考数学一诊试卷 题型:解答题
如图,已知△ABC中,D为AB的中点.
(1)请用尺规作图法作边AC的中点E,并连接DE(保留作图痕迹,不要求写作法);
(2)在(1)的条件下,若DE=4,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com