
一个不透明的口袋中装有形状大小相同的四个小球,每个小球上各标有一个数字,分别是1,2,3,4,现规定从袋中任意取出一个小球后,不放回,再任意取出一个小球,用画树状图(或列表)的方法,求两次取出的两个小球上数字之积是偶数的概率.
. 【解析】试题分析: 如图,按要求画出树状图,由图可知共有12种等可能结果,其中两次数字之积为偶数的有10种,由此可得所求概率为. 试题解析: 画树状图如下: 由树状图可知,共有12种等可能结果,其中数字之积是偶数的有10种, ∴两次取出的两个小球上数字之积是偶数的概率为.科目:初中数学 来源:2017年山东省中考数学二模试卷 题型:单选题
我市今年中考理、化实验操作考试,采用学生抽签方式决定自己的考试内容,规定:每一位考生必须在三个物理实验(用纸签A、B、C表示)和三个化学实验(用纸签D、E、F表示)中各抽取一个进行考试,小刚在看不到纸签的情况下,分别从中各随机抽取一个.小刚抽到物理实验B和化学实验F的概率是( )
A. 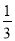 B.
B. 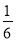 C.
C. 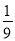 D.
D. 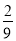
查看答案和解析>>
科目:初中数学 来源:福建省建瓯市2018届九年级数学上册期末测试卷 题型:解答题
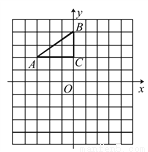
如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源:福建省建瓯市2018届九年级数学上册期末测试卷 题型:单选题
如图,△ABC内接于⊙O,AB=BC,∠ABC=120°,AD为⊙O的直径,AD=6,那么AB的值为( )
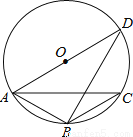
A. 3 B. 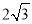 C. 3
C. 3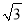 D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源:2017年吉林省长春市中考数学模拟试卷 题型:解答题
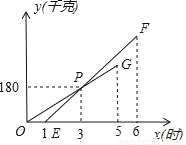
某家装公司聘请两队搬运工来搬运货物,他们都只能连续搬运5小时,甲队于某日0时开始搬运,过了1小时,乙队也开始搬运,如图,线段OG表示甲队搬运量y(千克)与时间x(时)的函数图象,线段EF表示乙队搬运量y(千克)与时间x(时)的函数图象.
(1)求乙队搬运量y与时间x之间的函数关系式.
(2)如果甲、乙两队各连续搬运5小时,那么乙队比甲队多搬运多少千克?
查看答案和解析>>
科目:初中数学 来源:2017年吉林省长春市中考数学模拟试卷 题型:填空题
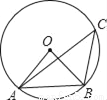
如图,A、B、C是⊙O上的三点,若∠C=30°,OA=3,则弧AB的长为_____.(结果保留π)
查看答案和解析>>
科目:初中数学 来源:2017年吉林省长春市中考数学模拟试卷 题型:单选题
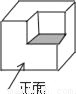
如图的几何体是由一个正方体切去一个小正方体形成的,它的主视图是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市七年级数学科期末检测模拟 题型:单选题
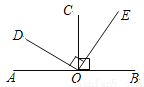
如图,CO⊥AB于点O,DO⊥EO,若∠DOC=58°40′,则∠BOE等于( )
A. 31°20′ B. 32°20′ C. 58°40′ D. 68°40′
C 【解析】∵DO⊥EO,CO⊥AB, ∴∠DOC+∠COE=90°, ∠BOE+∠COE=90°, ∴∠BOE=∠DOC=58°40′. 故选C.查看答案和解析>>
科目:初中数学 来源:山东省德州市2018届九年级上期末模拟数学试卷 题型:解答题
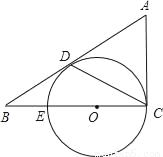
如图,△ABC中,∠ACB=90°,D是边AB上一点,且∠A=2∠DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.
(1)求证:AB是⊙O的切线;
(2)若CD的弦心距为1,BE=EO,求BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com