练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知两圆半径为5cm和3cm，圆心距为3cm，则两圆的位置关系是（ ）

    A．相交 B．内含 C．内切 D．外切

    A 【解析】 试题分析：圆心距为d，当R－r＜d＜R+r时，两圆相交；当d=R－r时，两圆内切；当d=R+r时，两圆外切；当0＜d＜R－r时，两圆内含；当d＞R+r时，两圆外离.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省丹阳市2017-2018学年七年级12月月考数学试卷 题型：解答题

    一个蓄水池有甲、乙两个进水管和一个丙排水管，单独开甲管6小时可注满水池；单独开乙管8小时可注满水池，单独开丙管9小时可将满池水排空，若先将甲、乙管同时开放2小时，然后打开丙管，问打开丙管后几小时可注满水池？

    打开丙管后小时可注满水池． 【解析】设打开丙管后x小时可注满水池．等量关系为：甲注水量+乙注水量-丙排水量=1． 据此列出方程并解答． 【解析】 设打开丙管后x小时可注满水池， 由题意得，（ +）（x+2）﹣x =1， 解这个方程， （x+2）﹣=1， 21x+42﹣8x=72， 13x=30， 解得x=． 答：打开丙管后小时可注满水池． ...

    查看答案和解析>>

    科目：初中数学 来源：广西贵港市港南区2017-2018学年七年级（上）期中数学试卷 题型：单选题

    买一个足球需要m元，买一个篮球需要n元，则买4个足球、7个篮球共需要（　　）元．

    A. 4m+7n B. 28mn C. 7m+4n D. 11mn

    A 【解析】已知一个足球需要m元，买一个篮球需要n元，可得买4个足球、7个篮球共需要（4m+7n）元，故选A.

    查看答案和解析>>

    科目：初中数学 来源：吉林省松原市2018届九年级上期末模拟数学试卷 题型：填空题

    从1，2，3这三个数字中任意抽取两个，其和是偶数的概率是________．

    【解析】首先根据题意画出树状图，然后由树状图求得所有等可能的结果与其和是偶数的情况，再利用概率公式即可求得答案． 【解析】 画树状图得： ∵共有6种等可能的结果，其和是偶数的2种情况， ∴其和是偶数的概率是：=． 故答案为：．

    查看答案和解析>>

    科目：初中数学 来源：吉林省松原市2018届九年级上期末模拟数学试卷 题型：单选题

    如图，在宽度为20m，长为32m的矩形地面上修筑同样宽的道路（图中阴影部分），余下的部分种上草坪，要使草坪的面积为540m2 ， 求道路的宽．如果设小路宽为xm，根据题意，所列方程正确的是（   ）

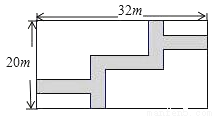
    A. （20+x）（32﹣x）=540 B. （20﹣x）（32﹣x）=100

    C. （20﹣x）（32﹣x）=540 D. （20+x）（32﹣x）=540

    C 【解析】【解析】 利用平移，原图可转化为下图，设小路宽为x米．根据题意得：（20﹣x）（32﹣x）=540．故选C．

    查看答案和解析>>

    科目：初中数学 来源：湖南省邵阳县黄亭市2017~2018学年九年级数学（上）期末检测模拟题 题型：解答题

    如图，某办公楼AB的后面有一建筑物CD，当光线与地面的夹角是22°时，办公楼在建筑物的墙上留下高2米的影子CE，而当光线与地面夹角是45°时，办公楼顶A在地面上的影子F与墙角C有25米的距离（B，F，C在一条直线上）．

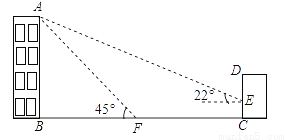
    （1）求办公楼AB的高度；

    （2）若要在A，E之间挂一些彩旗，请你求出A，E之间的距离．

    （参考数据：sin22°≈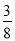，cos22°≈ 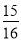，tan22°≈）

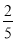    （1）教学楼的高20m；（2）A、E之间的距离约为48m． 【解析】（1）过点E作EM⊥AB于点M，设AB=x，在Rt△ABF中，由∠AFB=45°可知BF=AB=x， 在Rt△AEM中，利用锐角三角函数的定义求出x的值即可；（2）在Rt△AME中，根据cos22°=可得出结论． 【解析】 （1）过点E作EM⊥AB于点M，设AB=x， 在Rt△ABF中，∵∠AFB=45°...

    查看答案和解析>>

    科目：初中数学 来源：湖南省邵阳县黄亭市2017~2018学年九年级数学（上）期末检测模拟题 题型：填空题

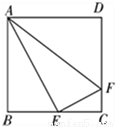
    如图，在正方形 ABCD 中，E 是BC 的中点，F 是CD 上一点，且CF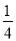＝CD，下列结论：①∠BAE＝30°；②△ABE∽△ECF；③AE⊥EF；④△ADF∽△ECF．其中正确结论是_____．(填序号)

    ②③ 【解析】设边长是4，则CF=1，DF=3，BE=EC=2，利用勾股定理知，AF=， 所以EF=，AE=. 所以 +=,所以AE⊥EF；③正确. ∠AEB+∠FEC=90°，∠CFE+∠FEC=90°，所以∠AEB=∠CFE，∠B=∠C, 所以△ABE∽△ECF②正确. 故答案为②③.

    查看答案和解析>>

    科目：初中数学 来源：湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型：解答题

    根据题意解答：（1）如图1的图形我们把它称为“8字形”，请说明∠A+∠B=∠C+∠D．

    （2）阅读下面的内容，并解决后面的问题： 如图2，AP、CP分别平分∠BAD、∠BCD，若∠ABC=36°，∠ADC=16°，求∠P的度数．

    解：∵AP、CP分别平分∠BAD、∠BCD

    ∴∠1=∠2，∠3=∠4

    由（1）的结论得：∠P+∠3=∠1+∠B①，∠P+∠2=∠4+∠D②，①+②，得2∠P+∠2+∠3=∠1+∠4+∠B+∠D

    ∴∠P= 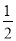（∠B+∠D）=26°．

    ①如图3，直线AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，若∠ABC=36°，∠ADC=16°，请猜想∠P的度数，并说明理由．

    ②在图4中，直线AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，猜想∠P与∠B、∠D的关系，直接写出结论，无需说明理由．

    ③在图5中，AP平分∠BAD，CP平分∠BCD的外角∠BCE，猜想∠P与∠B、∠D的关系，直接写出结论，无需说明理由．

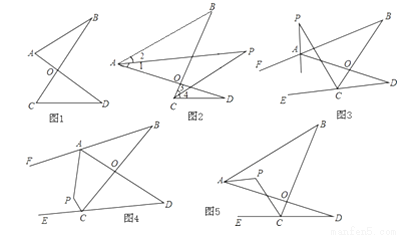
    （1）证明见解析；（2）①∠P=26゜；②∠P=180°﹣（∠B+∠D）；③∠P=90°+ （∠B+∠D）． 【解析】试题分析：（1）根据三角形的内角和等于180°列式整理即可得证； （2）根据角平分线的定义可得∠1=∠2，∠3=∠4，再根据（1）的结论列出整理即可得解；①表示出∠PAD和∠PCD，再根据（1）的结论列出等式并整理即可得解； ②根据四边形的内角和等于360°，可得...

    查看答案和解析>>

    科目：初中数学 来源：2017年安徽省六安市中考数学模拟试卷（4月份） 题型：单选题

    自来水公司调查了若干用户的月用水量x（单位：吨），按月用水量将用户分成A、B、C、D、E五组进行统计，并制作了如图所示的扇形统计图．已知除B组以外，参与调查的用户共64户，则所有参与调查的用户中月用水量在6吨以下的共有( )

    组别

    月用水量x（单位：吨）

    A

    0≤x<3

    B

    3≤x<6

    C

    6≤x<9

    D

    9≤x<12

    E

    x≥12

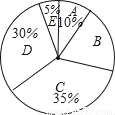
    A. 18户 B. 20户 C. 22户 D. 24户

    D 【解析】除B占以外比是30%-5%-10%-35%=80%，64户. 所以A，B为30%，8024户.故选D.

    查看答案和解析>>

    同步练习册答案