练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图所示,AB∥CD,试解决下列问题:

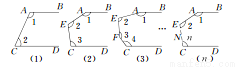
    (1)在图(1)中,∠1+∠2等于多少度?请说明理由;

    (2)在图(2)中∠1+∠2+∠3等于多少度?请说明理由;

    (3)在图(n)中,试探究∠1+∠2+∠3+∠4+…+∠n等于多少度.

    (1) ∠1+∠2=180°, 理由见解析; (2)∠1+∠2+∠3=360°,理由见解析; (3)∠1+∠2+∠3+∠4+…+∠n=180°(n- 1). 【解析】试题分析: （1）根据平行线的性质推出即可； （2）根据同旁内角互补，两直线平行推出即可； （3）根据（1）（2）的结果得出即可． 试题解析: (1)因为AB∥CD, 所以∠1+∠2=180°(两直...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山东省临沂市沂水县2017-2018学年八年级（上）期中数学试卷 题型：解答题

    如图，已知在四边形ABCD中，点E在AD上，∠BCE=∠ACD=90°，∠BAC=∠D，BC=CE．

    （1）求证：AC=CD；

    （2）若AC=AE，求∠DEC的度数．

    （1）证明见解析；（2）112.5°． 【解析】试题分析： 根据同角的余角相等可得到结合条件，再加上 可证得结论； 根据 得到 根据等腰三角形的性质得到 由平角的定义得到 试题解析： 证明： 在△ABC和△DEC中， ， （2）∵∠ACD＝90°，AC＝CD， ∴∠1＝∠D＝45°， ∵AE＝AC， ∴∠3＝∠5＝67.5°， ∴∠DEC＝180°... 复制答案 考点分析： 相关试题推荐

    如图，在直角坐标平面内，已知点A（8，0），点B（3，0），点C是点A关于直线m（直线m上各点的横坐标都为3）的对称点．

    （1）在图中标出点A，B，C的位置并求出点C的坐标；

    （2）如果点P在y轴上，过点P作直线l∥x轴，点A关于直线l的对称点是点D，那么当△BCD的面积等于10时，求点P的坐标．

    查看答案

    将一副直角三角板如图摆放，等腰直角板ABC的斜边BC与含30°角的直角三角板DBE的直角边BD长度相同，且斜边BC与BE在同一直线上，AC与BD交于点O，连接CD．

    求证：△CDO是等腰三角形．

    查看答案

    如图：△ABC和△ADE是等边三角形，AD是BC边上的中线．求证：BE=BD．

    查看答案

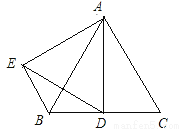
    如图，点C，F，E，B在一条直线上，∠CFD＝∠BEA，CE＝BF，DF＝AE，写出CD与AB之间的关系，并证明你的结论．

    查看答案

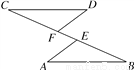
    如图，在△ABC中，CD是AB边上高，BE为角平分线，若∠BFC=113°，求∠BCF的度数．

    查看答案 试题属性
    • 题型：解答题
    • 难度：中等
    Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级上册 第五章 一元一次方程 5．1　认识一元一次方程 同步测试卷 含答案 题型：填空题

    已知方程(1＋a)x2＋2x－3＝2是关于x的一元一次方程，则a＝________.

    －1 【解析】根据一元一次方程的定义,未知数的最高指数是1,所以1+a=0,解得:a=－1, 故答案为: －1.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级上册 第三章 整式及其加减 3．3　整式 同步测试卷 含答案 题型：填空题

    下列式子中：①mn＋a；②ax2＋bx＋c；③－6ab；④ 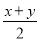；⑤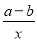；⑥5＋7x．整式有________．（填序号）

    ①②③④⑥ 【解析】①mn＋a是多项式也是整式；②ax2＋bx＋c是多项式也是整式；；③－6ab是单项式也是整式；④是多项式也是整式；；⑤是多项式也是整式；；⑥5＋7x是多项式也是整式；. 故答案为：①②③④⑥

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级上册 第三章 整式及其加减 3．3　整式 同步测试卷 含答案 题型：单选题

    下列说法正确的是（　　）

    A. 单项式x的系数和次数都是0

    B. 单项式x的系数和2的系数一样都是1

    C. 5πR2的系数为5

    D. 0是单项式

    D 【解析】根据单项式的系数和次数的定义： A.单项式x的系数是1，次数都是1，故本选项错误； B.单项式x的系数是1，2是常数项，2的系数不是1，故本选项错误； C.5πR2的系数为5π，π是常数，故本选项错误； D.0是单项式，正确. 故选：D.

    查看答案和解析>>

    科目：初中数学 来源：人教版数学七年级下册（贵州专版） 期中综合检测 题型：解答题

    将下列各数填入相应的集合内.

    - 7,0.32, 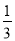,0, 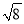,　,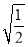,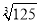π,0.1010010001….

    ①有理数集合{　　　　　　　　　　　…　}

    ②无理数集合{　　　　　　　　　　　…　}

    ③负实数集合{　　　　　　　　　　　…　}

    答案见解析 【解析】试题分析: 根据实数的分类：实数分为有理数、无理数．或者实数分为正实数、0、负实数．进行填空． 试题解析: ,. ①有理数集合{- 7,0.32, ,0, ,…} ②无理数集合{, ,π,0.1010010001…,…} ③负实数集合{- 7,…}

    查看答案和解析>>

    科目：初中数学 来源：人教版数学七年级下册（贵州专版） 期中综合检测 题型：填空题

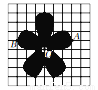
    如图所示,如果用(0,0)表示梅花的中心O,用(3,1)表示梅花上一点A,则梅花上点B可以用坐标____表示. 

    (- 3,1) 【解析】根据图形可以直接写出点B的坐标(- 3,1). 故答案为: (- 3,1).

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.2二次函数与一元二次方程 练习 题型：填空题

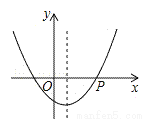
    如图，抛物线y=ax2+bx+c（a＞0）的对称轴是过点（1，0）且平行于y轴的直线，若点P（4，0）在该抛物线上，则4a﹣2b+c的值为_________．

    0 【解析】试题分析：设抛物线与x轴的另一个交点是Q，∵抛物线的对称轴是过点（1，0），与x轴的一个交点是P（4，0），∴与x轴的另一个交点Q（﹣2，0），把（﹣2，0）代入解析式得：0=4a﹣2b+c，∴4a﹣2b+c=0，故答案为：0．

    查看答案和解析>>

    科目：初中数学 来源：初一数学第一学期4.1线段、直线、射线 同步练习 题型：填空题

    已知线段MN，在MN上逐一画点（所画点与M、N不重合），当线段上有1个点时，共有3条线段，当线段上有2个点时，共有6条线段；当线段上有3个点时，共有10条线段；直接写出当线段上有20个点时，共有线段__条．

    210 【解析】根据题意可得:当在MN上有20个点时,共有线段:1+2+3+……+20=10×21=210, 故答案为:210.

    查看答案和解析>>

    同步练习册答案