练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    用反证法证明AB≠AC时，首先假设________成立．

    AB=AC 【解析】反证法的步骤是：（1）假设结论不成立；（2）从假设出发推出矛盾；（3）假设不成立，则结论成立． 由此可得用反证法证明AB≠AC时，首先假设AB=AC成立．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2018年春人教版八年级数学下册（广西）期末测试 题型：单选题

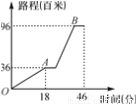
    某中学组织初一、初二学生举行“四城同创”宣传活动，从学校坐车出发，先上坡到达A地后，宣传8分钟；然后下坡到B地宣传8分钟返回，行程情况如图．若返回时，上、下坡速度保持不变，在A地仍要宣传8分钟，则他们从B地返回学校用的时间是（　　）

    A. 48分钟 B. 45.2分钟 C. 46分钟 D. 33分钟

    B 【解析】由上图可知，上坡的路程为3600米，速度为200米每分钟；下坡时的路程为6000米，速度为6000÷（46-18-8×2）=500米每分钟；由于返回时上下坡互换，变为上坡路程为6000米，所以所用时间为6000÷200=30分钟；下坡路程为3600米，所用时间是3600÷500=7.2分钟；又知在A地停8分钟；所以总时间为30+8+7.2=45.2分钟．故选B

    查看答案和解析>>

    科目：初中数学 来源：2017年广西南宁八中中考数学五模试卷 题型：解答题

    先化简，再求值：（1+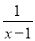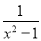）÷﹣（x﹣2），其中x=．

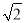    4 【解析】试题分析：先根据分式的混合运算和运算顺序，先通分，把除化为乘，再约分即可完成化简，再代入求值即可. 试题解析：【解析】 =， =x2+2， 当x=时，原式=）2+2=4．

    查看答案和解析>>

    科目：初中数学 来源：2017年广西南宁八中中考数学五模试卷 题型：单选题

    下列计算正确的是（　　）

    A. a2•a3=a6 B. （a+b）（a﹣2b）=a2﹣2b2

    C. （ab3）2=a2b6 D. 5a﹣2a=3

    C 【解析】试题分析：根据同底数幂的乘法法则、多项乘以多项式的法则、积的乘方和幂的乘方法则以及代理商的运算法则逐项进行计算，即可求得答案． 试题解析：A、a2•a3=a5，故本选项错误； B、（a+b）（a-2b）=a2—ab-2b2，故本选项错误； C、（ab3）2=a2b6,本选项正确； D、5a-2a=3a，故本选项错误． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：山西省2017-2018学年八年级上期末模拟数学试卷 题型：解答题

    如图，在?ABCD中，M，N在对角线AC上，且AM＝CN，求证：BM∥DN.

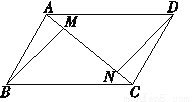
    证明见解析. 【解析】试题分析：连接BD、MD、BN，根据平行四边形的性质证明OM=ON，然后再证明四边形BNDM是平行四边形，从而可得BM∥DN． 试题解析：连接BD、MD、BN， ∵四边形ABCD是平行四边形， ∴OA=OC，OB=OD， ∵AM=CN， ∴OA-AM=OC-CN， 即OM=ON， ∴四边形BNDM是平行四边形． ∴BM∥D...

    查看答案和解析>>

    科目：初中数学 来源：山西省2017-2018学年八年级上期末模拟数学试卷 题型：填空题

    如图所示的一块地，已知AD=4m，CD=3m，∠ADC=90°，AB=13m，BC=12m，求这块地的面积．

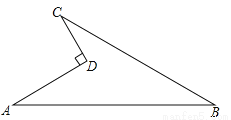
    24． 【解析】试题分析：连接AC，利用勾股定理及逆定理可以得出三角形ACD和ABC是直角三角形，△ABC的面积减去△ACD的面积就是所求的面积． 试题解析：【解析】 连接AC ． 在Rt△ACD中，AD=4，CD=3，∴AC 2 =AD 2 +CD 2 =4 2 +3 2 =25，又∵AC＞0，∴AC=5． 又∵BC=12，AB=13，∴AC 2 +BC 2 =5 2 ...

    查看答案和解析>>

    科目：初中数学 来源：山西省2017-2018学年八年级上期末模拟数学试卷 题型：单选题

    已知9x2+kxy+4y2是一个完全平方展开式，那么k的值是（   ）

    A. 12 B. 24 C. ±12 D. ±24

    C 【解析】已知9x2+kxy+4y2是一个完全平方展开式，中间一项为加上或减去3x和2y积的2倍，所以k=±12．故选C.

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年黑龙江省哈尔滨市松北区2017届九年级上学期期末数学试卷 题型：填空题

    不等式组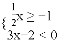的解集为________．

    【解析】 ∵解不等式①得：x??2， 解不等式②得：x<， ∴不等式组的解集为?2?x<， 故答案为：?2?x<.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷（C卷） 题型：解答题

    如图，等腰直角△ABC中，∠ABC=90°，点P在AC上，将△ABP绕顶点B沿顺时针方向旋转90°后得到△CBQ.

    (1)求∠PCQ的度数;

    (2)当AB=4，AP：BP=1：3时，求PQ的长；

    (3)当点P在线段AC上运动时(P不与A、C重合)，请写出一个反映PA2、PC2、PB2之间关系的等式，并加以证明.

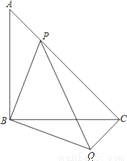
    （1）∠PCQ=90°；（2）PQ=；（3）2PB2=PA2+PC2. 【解析】试题分析：（1）由于∠PCB=∠BCQ=45°，故有∠PCQ=90°． （2）由等腰直角三角形的性质得到AC的长，根据已知条件，可求得AP，PC的值，再由勾股定理求得PQ的值． （3）由于△PBQ也是等腰直角三角形，故有PQ2=2PB2=PA2+PC2． 试题解析：【解析】 （1）由题意知，△...

    查看答案和解析>>

    同步练习册答案