
���м�����ȷ���ǣ�������
A. a2•a3=a6 B. ��a+b����a��2b��=a2��2b2
C. ��ab3��2=a2b6 D. 5a��2a=3
C ���������������������ͬ�����ݵij˷���������Զ���ʽ�ķ����ij˷����ݵij˷������Լ������̵����㷨��������м��㣬������ô𰸣� ���������A��a2•a3=a5���ʱ�ѡ����� B����a+b����a-2b��=a2��ab-2b2���ʱ�ѡ����� C����ab3��2=a2b6,��ѡ����ȷ�� D��5a-2a=3a���ʱ�ѡ����� ��ѡC�� ���ɶ��ȫ���ƿؾ�ϵ�д�
���ɶ��ȫ���ƿؾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2018�괺�˽̰���꼶��ѧ�²ᣨ��������ĩ���� ���ͣ������
ijУҪ��С����С������ͬѧ����ѡһ�˲μ�ȫ��֪ʶ����������������ѡ�β����У������ijɼ��ֱ����±���
���� | 1 | 2 | 3 | 4 | 5 |
�� | 60 | 75 | 100 | 90 | 75 |
�� | 70 | 90 | 100 | 80 | 80 |
�����ϱ�����������⣺
��1������±���
���� | ƽ���ɼ����֣� | ��λ�����֣� | �������֣� | ���� |
�� | 80 | 75 | 75 | 190 |
�� |
��2��������β����У��ɼ��Ƚ��ȶ���ͬѧ��˭������80�����ϣ���80�֣��ijɼ���Ϊ���㣬��С����С��������β����е������ʸ��Ƕ��٣�
��3����������������ɼ��ﵽ80�����ϣ���80�֣��ͺܿ��ܻ��ɼ��ﵽ90�����ϣ���90�֣��ͺܿ��ܻ��һ�Ƚ�����ô����Ϊѡ˭�μӱ����ȽϺ��ʣ�˵��������ɣ�
��1��84 80 80 104����2����С����������Ϊ40%.С���������Ϊ80%����3��С����ɼ����� �������������������1������ƽ��������λ��������������ĸ����ʽ���ɵó��𰸣���2�����ݷ�������弴���ӳ���ݵIJ����̶ȣ��ó�����ԽСԽ�ȶ���Ӧ��С��ijɼ��ȶ������ݱ��е����ݷֱ���������ʼ��ɣ���3����ΪС��ijɼ���С���ijɼ��ȶ����������ʱ�С���ĸߣ����ѡС��μӱ����ȽϺ��ʣ�...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ��Ȱ��꼶�������¿���ѧ�Ծ� ���ͣ���ѡ��
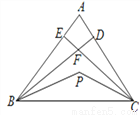
��ͼ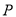 Ϊ
Ϊ ��һ�㣬
��һ�㣬 
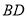 ��
��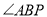 ��ƽ���ߣ�
��ƽ���ߣ� 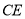 ��
��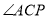 ��ƽ���ߣ�
��ƽ���ߣ� 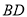 ��
��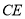 ����
����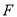 ,��
,��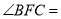 �� ��
�� ��
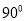
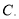
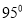
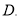
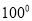
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��������������п���ѧ��ģ�Ծ� ���ͣ������
���о����У�������������ƴ��ƽ���ı��κ����Σ�����ƴ�������ε���ͼ��_____������ͼ������Ĵ��ţ��𰸸�ʽ�磺���٣��ڣ��ۣ��ܣ��ݡ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��������������п���ѧ��ģ�Ծ� ���ͣ���ѡ��
���˾����һ�ֽ���Ϊ21Ԫ�ĵ��Ӳ�Ʒ������۵ľ������ۣ��Կɻ���20%�������ֵ��Ӳ�Ʒ�ı��Ϊ(����)
A. 26Ԫ B. 27Ԫ C. 28Ԫ D. 29Ԫ
C ������������������������⣬����Ӳ�Ʒ�ı��ΪxԪ�����յ�����ϵ����ۡ�0.9������=���ۡ�20%�����г�һԪһ�η��̵ã�0.9x��21=21��20%��ã�x=28�������ֵ��Ӳ�Ʒ�ı��Ϊ28Ԫ�� ��ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ2017-2018ѧ����꼶����ĩģ����ѧ�Ծ� ���ͣ������
��ͼ����·��A��B�������25 km��C��DΪ����ׯ��DA��AB�ڵ�A��CB��AB�ڵ�B����֪DA��15 km��CB��10 km������Ҫ����·AB�Ͻ�һ�����ز�Ʒ�չ�վE��ʹ��C��D���嵽Eվ�ľ�����ȣ���EվӦ������Aվ����ǧ�״���
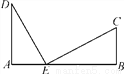
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ2017-2018ѧ����꼶����ĩģ����ѧ�Ծ� ���ͣ������
�÷�֤��֤��AB��ACʱ�����ȼ���________������
AB=AC ����������֤���IJ����ǣ���1��������۲���������2���Ӽ�������Ƴ�ì�ܣ���3�����費����������۳����� �ɴ˿ɵ��÷�֤��֤��AB��ACʱ�����ȼ���AB=AC�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�������ʡ���������ɱ���2017����꼶��ѧ����ĩ��ѧ�Ծ� ���ͣ������
��ͼ��������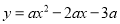 ��X���ڵ�A��B��A��B�ң�����Y���ڵ�C��
��X���ڵ�A��B��A��B�ң�����Y���ڵ�C�� 
=6����PΪ��һ�������������ϵ�һ��.
��1���������ߵĽ���ʽ��
��2������PCB=45�㣬���P�����ꣻ
��3����QΪ������������������һ�㣬��Q�ĺ�����ȵ�P�ĺ������1������PC��
AQ����PC=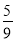 AQʱ�����P�������Լ���PCQ�����.
AQʱ�����P�������Լ���PCQ�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������ʡ��ɽ��2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
��ͼ��x�ᡢy������������ֱ���A(0,4)B(3,0)������x������һ��C��ʹ��ABCΪ���������Σ������������ĵ�C�У� ����
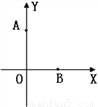
A. 2�� B. 3�� C. 4�� D. 5��
C ������������AP=AB����AΪԲ�ģ�ABΪ�뾶������x����1�����㣨A����⣩���������ABP�ǵ��������ε�P����1��������BP=AB����BΪԲ�ģ�BAΪ�뾶������x����2�����㣬�������ABP�ǵ��������ε�P����2��������PA=PB����AB�Ĵ�ֱƽ������x��ֻ��һ�����㣬�������ABP�ǵ��������ε�P����1�������Ե�P��x���ϣ���ABP�ǵ��������Σ����������ĵ�P����4������ѡC.�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com