
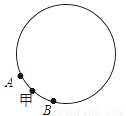
如图,A和B两个小机器人,自甲处同时出发相背而行,绕直径为整数米的圆周上运动,15分钟内相遇7次,如果A的速度每分钟增加6米,则A和B在15分钟内相遇9次,问圆周直径至多是多少米?至少是多少米?(取π=3.14)
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:浙江杭州西湖区保俶塔实验学校2018届九年级上学期期中考试数学试卷(含解析) 题型:解答题
如图,  内接于⊙
内接于⊙ ,
,  于
于 ,
, 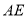 是⊙
是⊙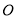 的直径,若
的直径,若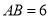 ,
,  ,
, 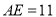 .
.
(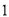 )求证:
)求证:  .
.
( )求
)求 的长.
的长.

查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年八年级12月月考数学试卷 题型:单选题
下列各数: 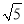 ,
, 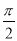 ,
, 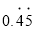 ,0,-
,0,- 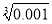 ,9.181181118,其中无理数有( )
,9.181181118,其中无理数有( )
A. 1个 B. 2个 C. 3个 D. 4个
B 【解析】因为无理数包括无限不循环小数,开方开不尽的数,所以,,是无理数,故选B.查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型:单选题
不等式组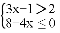 的解集在数轴上表示为( )
的解集在数轴上表示为( )
A. 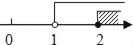 B.
B. 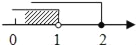 C.
C. 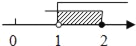 D.
D. 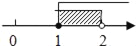
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型:单选题
如图,等腰三角形ABC中,∠BAC=90°,在底边BC上截取BD=AB,过D作DE⊥BC交AC于E,连接AD,则图中等腰三角形的个数是( )
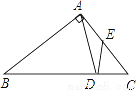
A. 1 B. 2 C. 3 D. 4
D 【解析】三角形ABC是等腰三角形,且∠BAC=90°,所以∠B=∠C=45°,又DE⊥BC,所以∠DEC=∠C=45°,所以△EDC是等腰三角形,BD=AB,所以△ABD是等腰三角形,∠BAD=∠BDA,而∠EAD=90°﹣∠BAD,∠EDA=90°﹣∠BDA,所以∠EAD=∠EDA,所以△EAD是等腰三角形,因此图中等腰三角形共4个. 故选:D.查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型:填空题
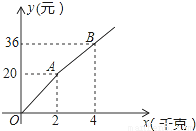
如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省________元.
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型:单选题
小王计划用100元钱买乒乓球,所购买球的个数W(个)与单价n(元)的关系式w= 中( )
中( )
A. 100是常量,W,n 是变量 B. 100,W是常量,n 是变量
C. 100,n是常量,W是变量 D. 无法确定
A 【解析】根据变量和常量的定义:在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量,可由小王计划用100元钱买乒乓球,所购买球的个数W(个)与单价n(元)的关系式w=中100是常量,W,n 是变量, 故选:A.查看答案和解析>>
科目:初中数学 来源:湖南省邵阳县黄亭市2017~2018学年九年级数学(上)期末综合检测模拟题 题型:填空题
已知一元二次方程x2 +3x-4=0的两根为x1,x2,则x12+ x1x2+ x12=_____.
13 【解析】∵方程有两个实数根, ∴. ∴.查看答案和解析>>
科目:初中数学 来源:2017年甘肃省兰州市中考数学模拟试卷 题型:单选题
如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( )
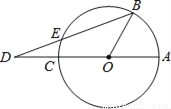
A. DE=EB B. 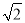 DE=EB C.
DE=EB C. 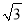 DE=DO D. DE=OB
DE=DO D. DE=OB
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com