
如图,  内接于⊙
内接于⊙ ,
,  于
于 ,
, 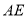 是⊙
是⊙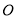 的直径,若
的直径,若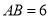 ,
,  ,
, 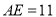 .
.
(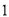 )求证:
)求证:  .
.
( )求
)求 的长.
的长.

科目:初中数学 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:单选题
二次函数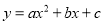 图象上部分点的坐标满足下表,则该函数图象的顶点坐标为
图象上部分点的坐标满足下表,则该函数图象的顶点坐标为
X | … | -3 | -2 | -1 | 0 | 1 | … |
y | … | -3 | -2 | -3 | -6 | -11 | … |
A. (﹣3,﹣3) B. (﹣2,﹣2) C. (﹣1,﹣3) D. (0,﹣6)
B 【解析】∵x=?3和?1时的函数值都是?3相等, ∴二次函数的对称轴为直线x=?2, ∴顶点坐标为(?2,?2). 故选:B.查看答案和解析>>
科目:初中数学 来源:2017年河南省中考数学三模试卷 题型:填空题
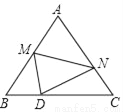
如图,等边△ABC的边长为10,点M是边AB上一动点,将等边△ABC沿过点M的直线折叠,该直线与直线AC交于点N,使点A落在直线BC上的点D处,且BD:DC=1:4,折痕为MN,则AN的长为_____.
查看答案和解析>>
科目:初中数学 来源:湖北省黄冈市2017-2018学年七年级上学期第三次学力检测数学试卷 题型:单选题
随着服装市场竞争日益激烈,某品牌服装专卖店一款服装按原售价降价a元后,再次降价20%,现售价为b元,则原售价为( )
A. (a+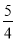 b)元 B. (a+
b)元 B. (a+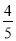 b)元 C. (b+
b)元 C. (b+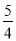 a)元 D. (b+
a)元 D. (b+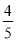 a)元
a)元
查看答案和解析>>
科目:初中数学 来源:湖北省黄冈市2017-2018学年七年级上学期第三次学力检测数学试卷 题型:单选题
下列各对数是互为倒数的是( )
A. 4和-4 B. -3和 C. -2和
C. -2和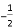 D. 0和0
D. 0和0
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区保俶塔实验学校2018届九年级上学期期中考试数学试卷(含解析) 题型:填空题
如图,正方形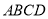 的顶点
的顶点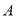 ,
, 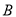 与正方形
与正方形 的顶点
的顶点 ,
, 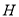 同在一段抛物线上,且抛物线的顶点同时落在
同在一段抛物线上,且抛物线的顶点同时落在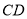 和
和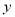 轴上,正方形的边
轴上,正方形的边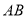 与
与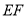 同时落在
同时落在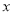 上.若正方形
上.若正方形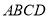 的边长为
的边长为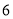 ,则正方形
,则正方形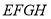 的边长为__________.
的边长为__________.
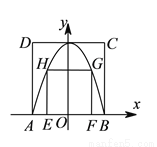
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区保俶塔实验学校2018届九年级上学期期中考试数学试卷(含解析) 题型:单选题
有一座圆弧形的拱桥,桥下水平宽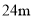 ,拱顶高出水平面
,拱顶高出水平面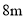 ,现有一货船,送一箱货欲从桥下经过,已知货箱(货箱底与水平面持平)宽
,现有一货船,送一箱货欲从桥下经过,已知货箱(货箱底与水平面持平)宽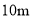 ,至多能截( )
,至多能截( )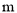 的货.
的货.
A. 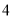 B.
B. 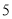 C.
C. 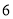 D.
D. 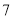
查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年八年级12月月考数学试卷 题型:单选题
一次函数y=kx+b的图象只经过第一、二、三象限,则( )
A. k<0,b>0 B. k>0,b>0 C. k>0,b<0 D. k<0,b<0
B 【解析】因为一次函数y=kx+b的图象只经过第一,二,三象限,所以k>0,b>0,故选B.查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型:解答题
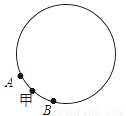
如图,A和B两个小机器人,自甲处同时出发相背而行,绕直径为整数米的圆周上运动,15分钟内相遇7次,如果A的速度每分钟增加6米,则A和B在15分钟内相遇9次,问圆周直径至多是多少米?至少是多少米?(取π=3.14)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com