
比较下列各组数大小:(Ⅰ)π________3.14 (Ⅱ) 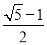 ________0.5.
________0.5.
科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷一 题型:单选题
已知抛物线y=﹣x2+1的顶点为P,点A是第一象限内该二次函数图象上一点,过点A作x轴的平行线交二次函数图象于点B,分别过点B、A作x轴的垂线,垂足分别为C、D,连结PA、PD,PD交AB于点E,△PAD与△PEA相似吗?( )
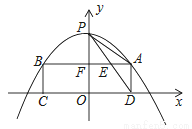
A. 始终不相似 B. 始终相似 C. 只有AB=AD时相似 D. 无法确定
B 【解析】试题分析:设A(x,-+1)根据题意可求出PA、PD、PE的值,从而得出PE:PA=PA:PD,又∠APE=∠DPA,因此,△PAD∽△PEA.查看答案和解析>>
科目:初中数学 来源:人教版七年级下册数学第7-10章综合测试卷 题型:填空题
在一次抽样调查中收集了一些数据,对数据进行分组,绘制了频数分布表,由于操作失误,绘制时不慎把第三小组的频数弄丢了,现在只知道最后一组(89.5~99.5)出现的百分比为15%,由此可知丢失的第三小组的频数是________
分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~99.5 |
频数 | 9 | 15 | ? | 16 | 12 |
查看答案和解析>>
科目:初中数学 来源:人教版七年级下册数学第6章实数单元检测卷 题型:解答题
已知x+12的算术平方根是 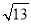 ,2x+y﹣6的立方根是2.
,2x+y﹣6的立方根是2.
(1)求x,y的值;
(2)求3xy的平方根.
(1)x=1,y=12;(2)±6 【解析】试题分析:(1)根据算术平方根、立方根的定义解答,由算数平方根的定义,可得x+12=()2,求解可得到x的值;由立方根的定义,得到2x+y-6=23,将x的值代入2x+y=14,即可得到y的值;(2)先求出3xy的值,再结合平方根的定义即可求出3xy平方根. (1)【解析】 ∵x+12的算术平方根是 ,2x+y﹣6的立方根是2. ∴x+12...查看答案和解析>>
科目:初中数学 来源:人教版七年级下册数学第6章实数单元检测卷 题型:单选题
下列结论正确的是( )
A. 64的立方根是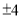 B.
B. 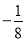 没有立方根
没有立方根
C. 立方根等于本身的的数是0 D. 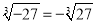
查看答案和解析>>
科目:初中数学 来源:北师大版数学九年级下册 1.1 锐角三角函数 题型:单选题
如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )

A. 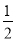 B.
B. 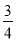 C.
C. 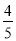 D.
D. 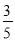
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区公益中学2018届九年级上学期期中数学试卷 题型:填空题
实数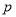 ,
, 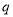 ,用符号
,用符号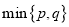 表示
表示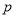 ,
, 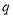 两数中较小的数,如
两数中较小的数,如 ,因此,若
,因此,若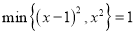 ,则
,则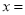 __________.若
__________.若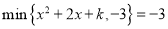 ,则
,则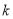 满足__________.
满足__________.
查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册数学 第五章 生活中的轴对称 单元检测卷 题型:解答题
如图,草原上,一牧童在A处放马,牧童家在B处,A、B处距河岸的距离AC,BD的长分别为500m和700m,且CD=500m,天黑前牧童从A点将马牵到河边去饮水后,再赶回家,牧童将马牵到河边什么地方饮水,才能使走过的路程最短?牧童最少要走多少m?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com