练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

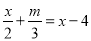    方程与方程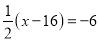的解相同，则m的值为_____．

    －6 【解析】【解析】 去分母得：x﹣16=﹣12 去括号、合并同类项得：x=4． 把x=4代入方程，得：2+=4﹣4，解得m=﹣6．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：广东省2017-2018学年七年级（上）期末模拟数学试卷 题型：单选题

    下列计算正确的是（    ）

    A. 3a－2b＝a                    B. 5y－3y＝2                    C. 7a＋a＝7a2                    D. 3x2y－2yx2＝x2y

    D 【解析】A.3a与2b不是同类项，无法合并，选项错误； B.5y－3y＝2y，选项错误； C.7a＋a＝8a，选项错误； D.3x2y－2yx2＝3x2y-2x2y=x2y，本选项正确. 选D

    查看答案和解析>>

    科目：初中数学 来源：江苏省南通市崇川区2015-2016学年七年级上学期期末考试数学试卷 题型：填空题

    设a，b，c，d为实数，现规定一种新的运算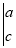 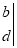=ad-bc，则满足等式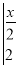 =1的x的值为 ．

    -10 【解析】 试题分析：根据题中的新定义化简已知方程，求出方程的解即可得到x的值． 试题解析：根据题中的新定义得： 去分母得：3x-4x-4=6， 移项合并得：-x=10， 解得：x=-10

    查看答案和解析>>

    科目：初中数学 来源：江苏省南通市崇川区2016-2017学年七年级上学期期末考试数学试卷 题型：解答题

    按顺序完成一下运算：

    ①取任一个三位数，使它的首位和末位的差大于1；

    ②交换首位和末位数字而构成另一个数；

    ③求此两个三位数的差；

    ④颠倒这个差的各位数字的次序，又构成一个新的数；

    ⑤将第三步所得的数与第四步所得的数加到一起．

    现在，我们可以得到最后的结果一定是1089．

    为什么最后结果一定是1089，请说明理由．

    答案见解析． 【解析】试题分析：根据题意可以将原来的三位数表示出来，然后根据①②③④⑤的要求进行变形，最后求出结果即可． 试题解析：【解析】 不妨用a，b，c代表一个三位数的百位上的数、十位上的数和个位上的数，则：①这个三位数可表示为100a＋10b＋c； ②交换首位和末位数字，得到另一个数100c＋10b＋a； ③两个三位数的差为：（100a＋10b＋c）－（100c＋...

    查看答案和解析>>

    科目：初中数学 来源：江苏省南通市崇川区2016-2017学年七年级上学期期末考试数学试卷 题型：解答题

    求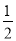x－2（x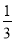－y2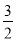）＋（－x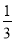＋y2）的值，其中x＝－2，y＝．

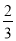    －3x＋y2， ． 【解析】试题分析：此题是整式的化简求值问题，先根据去括号，合并同类项进行化简，再把已知的值代入求值． 试题解析： = =-3x+ 当x=-2，y=时，原式=-3×（-2）+ =6+ =

    查看答案和解析>>

    科目：初中数学 来源：江苏省南通市崇川区2016-2017学年七年级上学期期末考试数学试卷 题型：单选题

    如果一个多项式的各项的次数都相同，则称该多项式为齐次多项式．例如：x3＋2xy2＋2xyz＋y3是3次齐次多项式．若xm+2y2＋3xy3z2是齐次多项式，则m等于（　　）

    A. 1 B. 2 C. 3 D. 4

    B 【解析】【解析】 由题意，得m+2+2=6，解得m=2．故选B．

    查看答案和解析>>

    科目：初中数学 来源：江苏省南通市崇川区2016-2017学年七年级上学期期末考试数学试卷 题型：单选题

    已知x＝y，则下面变形错误的是（　　）

    A. x＋a＝y＋a B. x－a＝y－a C. 2x＝2y D.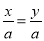

    D 【解析】解：A．B、C的变形均符合等式的基本性质，D项a不能为0，不一定成立．故选D．

    查看答案和解析>>

    科目：初中数学 来源：黑龙江省大庆市2016-2017下学期初一期末数学试卷 题型：填空题

    如图，把一张长方形的纸按图那样折叠后，B、D两点落在B′、D′点处，若得∠AOB′=80°, 则∠B′OG的度数为__________.

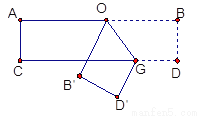
    50° 【解析】【解析】 ∵∠AOB′=80°，∴∠B′OB=180°﹣80°=100°，∵把一张长方形的纸按图那样折叠后，B、D两点落在B′、D′点处，∴∠B′OG=∠BOG=∠BOB′=50°，故答案为：50°．

    查看答案和解析>>

    科目：初中数学 来源：云南省2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

    在△ABC中，BC=AC，∠BCA=90°，P为直线AC上一点，过点A作AD⊥BP于点D，交直线BC于点Q．

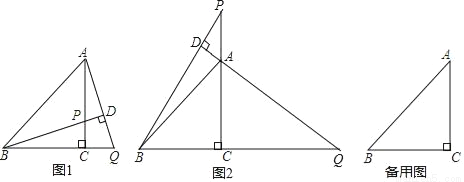
    （1）如图1，当P在线段AC上时，求证：BP=AQ；

    （2）如图2，当P在线段CA的延长线上时，（1）中的结论是否成立？　 　（填“成立”或“不成立”）

    （3）在（2）的条件下，当∠DBA=　 　度时，存在AQ=2BD，说明理由．

    （1）证明见解析；（2）（2）成立，理由见解析；（3）当∠DBA=22.5°时，存在AQ=2BD，理由见解析. 【解析】试题分析：（1）首先根据内角和定理得出∠DAP=∠CBP，进而得出 △ACQ≌△BCP即可得出答案； （2）延长BA交PQ于H，由于 得到 推出△AQC≌△BPC(ASA)，即可得出结论； （3）当时，存在根据等腰三角形的性质得到BP=2BD，通过△PBC≌△AC...

    查看答案和解析>>

    同步练习册答案