练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

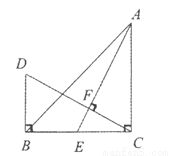
    如图，△ABC中，∠ACB=90°，AC=BC，AE是BC边上的中线，过点C作CF⊥AE，垂足为点F，过点B作BD⊥BC交CF的延长线于点D，BD=2，则△ABE的面积为________.

    4 【解析】∵DB⊥BC，AE⊥CD， ∴∠DBC=∠ACE=∠AFC=90°， ∵∠DCB+∠ACF=90°,∠ACF+∠EAC=90°， ∴∠DCB=∠EAC， ∵BC=AC， ∴△DBC≌△ECA， ∴DB=EC=2， ∵BE=EC， ∴BE=EC=2，AC=BC=4， ∴S△ABE=?BE?AC=×2×4=4. 故答案为：4...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：重庆市江津区2017届九年级下学期期末考试数学试卷 题型：单选题

    如图，四边形PAOB是扇形OMN的内接矩形，顶点P在上，且不与M，N重合，当P点在上移动时，矩形PAOB的形状、大小随之变化，则AB的长度（ ）

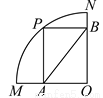
    A. 变大 B. 变小 C. 不变 D. 不能确定

    C 【解析】试题解析：∵PAOB是扇形OMN的内接矩形， ∴AB=OP=半径， 当P点在上移动时，半径一定，所以AB长度不变， 故选C．

    查看答案和解析>>

    科目：初中数学 来源：山东省无棣县2017-2018学年八年级上学期期中考试数学试卷. 题型：填空题

    如图，在Rt△ABC与Rt△DCB中，已知∠A=∠D=90°，请你添加一个条件（不添加字母和辅助线），使Rt△ABC≌Rt△DCB，你添加的条件是______．

    AB=DC． 【解析】【解析】 ∵斜边与直角边对应相等的两个直角三角形全等，∴在Rt△ABC与Rt△DCB中，已知∠A=∠D=90°，使Rt△ABC≌Rt△DCB，添加的条件是：AB=DC．故答案为：AB=DC．

    查看答案和解析>>

    科目：初中数学 来源：北京四中2017-2018学年上学期初中八年级期中考试数学试卷 题型：解答题

    分解因式：

    （1）x2-y2+4y-4=_______________________；

    （2）x2-4xy+4y2-2x+4y-3=__________________.

    （x+y-2）（x-y+2）； （x-2y-3）（x-2y+1）. 【解析】试题分析: (1) 原式后三项结合，利用完全平方公式分解，再利用平方差公式分解即可． (2)首先分组得出（x-2y）2-2（x-2y）-3，进而利用因式分解法得出即可． 试题解析: (1) x2-y2+4y-4=x ²?(y ²?4y+4)=x ²?(y?2) ²=(x+y?2)(x?y+2) ...

    查看答案和解析>>

    科目：初中数学 来源：北京四中2017-2018学年上学期初中八年级期中考试数学试卷 题型：解答题

    解分式方程： .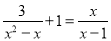

    x=3 【解析】试题分析：分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解． 试题解析：【解析】 去分母得：3+x2﹣x=x2，解得：x=3，经检验x=3是分式方程的解．

    查看答案和解析>>

    科目：初中数学 来源：北京四中2017-2018学年上学期初中八年级期中考试数学试卷 题型：填空题

    若分式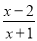的值为0，则x的值为___________.

    2 【解析】由题意可得：x?2=0且x+1≠0， 解得x=2. 故答案为:2.

    查看答案和解析>>

    科目：初中数学 来源：北京四中2017-2018学年上学期初中八年级期中考试数学试卷 题型：单选题

    已知x=3是分式方程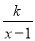=3的解，那么实数k的值为（ ）.

    A. 1 B. 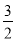C. 6 D. 9

    C 【解析】根据分式方程的根为x=3，可直接代入原方程=3得，解这个方程可得k=6. 故选：C.

    查看答案和解析>>

    科目：初中数学 来源：山西省2018届九年级上期末模拟数学试卷 题型：填空题

    已知一元二次方程x2+mx+m﹣1=0有两个相等的实数根，则m=_____．

    2． 【解析】试题分析：已知关于x的一元二次方程x2﹣mx+m﹣1=0有两个相等的实数根，可得△=b2﹣4ac=m2﹣4×1×（m﹣1）=m2﹣4m+4=（m﹣2）2=0，解得m=2.

    查看答案和解析>>

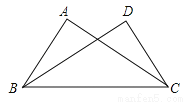
    科目：初中数学 来源：山东省临沂市费县2017-2018学年八年级（上）期中数学试卷 题型：解答题

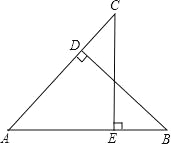
    如图，BD⊥AC于点D，CE⊥AB于点E，AD=AE．求证：BE=CD．

    证明过程见解析 【解析】 试题分析：要证明BE=CD，只要证明AB=AC即可，由条件可以求得△AEC和△ADB全等，从而可以证得结论． 试题解析：∵BD⊥AC于点D，CE⊥AB于点E， ∴∠ADB=∠AEC=90°， 在△ADB和△AEC中， ∴△ADB≌△AEC（ASA） ∴AB=AC， 又∵AD=AE， ∴BE=CD．

    查看答案和解析>>

    同步练习册答案