练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图所示，在下列条件中，不能判断△ABD≌△BAC的条件是（ ）

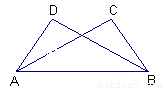
    A. ∠D=∠C，∠BAD=∠ABC B. BD=AC，∠BAD=∠ABC

    C. ∠BAD=∠ABC，∠ABD=∠BAC D. AD=BC，BD=AC

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省等六校2018届九年级12月月考数学试卷 题型：解答题

    已知二次函数y=x2-2x-3.

    （1）求函数图象的顶点坐标，与x轴和y轴的交点坐标，并画出函数的大致图象；

    （2）根据图象直接回答：当x满足 时，y＜0；当-1＜x＜2时，y的范围是 ．

    查看答案和解析>>

    科目：初中数学 来源：江苏省2017-2018学年八年级12月月考数学试卷 题型：单选题

    如图，Rt△ABC中，∠C=90°，AC=3，BC=4，AB=5，AD平分∠BAC．则S△ACD：S△ABD=（　　）

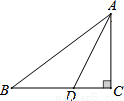
    A. 3：4 B. 3：5 C. 4：5 D. 1：1

    查看答案和解析>>

    科目：初中数学 来源：重庆市2017-2018学年八年级上学期第三次月考数学试卷 题型：填空题

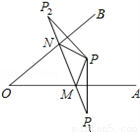
    如图所示，点P为∠AOB内一点，分别作出P点关于OA、OB的对称点P1，P2，连接P1P2交OA于M，交OB于N，P1P2=15，则△PMN的周长为__________．

    查看答案和解析>>

    科目：初中数学 来源：重庆市2017-2018学年八年级上学期第三次月考数学试卷 题型：单选题

    用大小相同的小三角形摆成如图所示的图案，按照这样的规律摆放，则第12个图案中共有小三角形的个数是（　　）

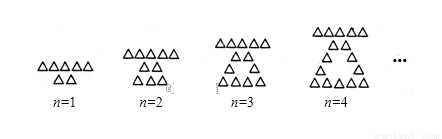
    A. 34 B. 40 C. 37 D. 35

    查看答案和解析>>

    科目：初中数学 来源：湖北省2017-2018学年七年级12月月考数学试卷 题型：解答题

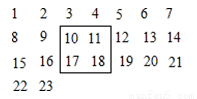
    把2100个连续的正整数1、2、3、……、2100，按如图方式排列成一个数表，如图用一个正方形框在表中任意框住4个数，设左上角的数为x．

    （1） 另外三个数用含x的式子表示出来，从小到大排列是___________

    （2） 被框住4个数的和为416时，x值为多少？

    （3） 能否框住四个数和为324？若能，求出x值；若不能，说明理由

    （4） 从左到右，第1至第7列各数之和分别为a1、a2、a3、a4、a5、a6、a7，请直接写出7个数中最大的数与最小的数之差．

    查看答案和解析>>

    科目：初中数学 来源：湖北省2017-2018学年七年级12月月考数学试卷 题型：填空题

    已知（a＋1）2＋|b＋5|＝b＋5，且|2a－b－1|＝1，则ab＝___________．

    查看答案和解析>>

    科目：初中数学 来源：江苏省东台市第四教育联盟2018届九年级上学期第二次质量检测（12月月考）数学试卷 题型：解答题

    已知正方形ABCD的边长为8，点E为BC的中点，连接AE，并延长交射线DC于点F，将△ABE沿着直线AE翻折，点B落在B′处，延长AB′，交直线CD于点M．

    （1）判断△AMF的形状并证明；

    （2）将正方形变为矩形ABCD，且AB=6，BC=8，若B′恰好落在对角线AC上时，得到图2，此时CF=_____， =_____；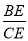

    （3）在（2）的条件下，点E在BC边上．设BE为x，△ABE沿直线AE翻折后与矩形ABCD重合的面积为y，求y与x之间的函数关系式．

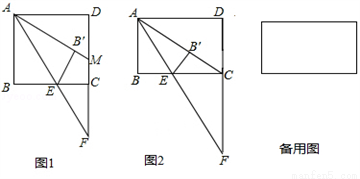
    【答案】（1）△AMF是等腰三角形，理由见解析；（2）10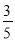， ；（3） .

    【解析】试题分析：（1）利用正方形的性质，∠BAE=∠F，又因为∠BAE=∠MAE，所以可得，△AMF是等腰三角形．AC=CF，

    （2）由（1）结论可知, ∴CF=AC=10，利用∠ACB的正弦求值.

    (3)分类讨论，当0＜x≤6时，△ABE翻折后都在矩形内部，所以重合部分面积就是三角形面积；当6＜x≤8时，设EB交AD于M，重叠部分的面积=△ABE的面积减去△AB′M的面积，得到函数解析式.

    试题解析：

    【解析】
    （1）结论：△AMF是等腰三角形．理由如下：

    如图1中，

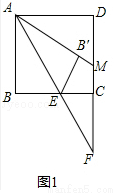
    ∵四边形ABCD是正方形，

    ∴AB∥DF，

    ∴∠BAE=∠F，

    由翻折可知∠BAE=∠MAE，

    ∴∠F=∠MAE，

    ∴MA=MF，

    ∴△AMF是等腰三角形．

    （2）如图2中，

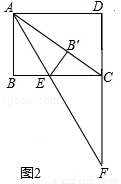
    由（1）可知△ACF是等腰三角形，AC=CF，

    在Rt△ABC中，∵AB=6，BC=8，

    ∴AC=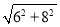=10，

    ∴CF=AC=10，

    ∵BE=BE′，

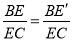    ∴=sin∠ACB=，

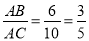    故答案为10， ．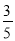

    （3）①如图3中，当0＜x≤6时，△ABE翻折后都在矩形内部，所以重合部分面积就是三角形面积，

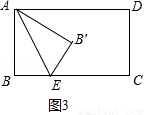
    ∴y=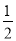•6•x=3x，

    ∴y=3x．

    ②如图4中，当6＜x≤8时，设EB交AD于M，

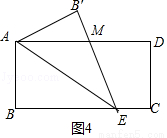
    ∴重叠部分的面积=△ABE的面积减去△AB′M的面积，

    设B′M=a，则EM=x﹣a，AM=x﹣a，

    在Rt△AB′M中，由勾股定理可得62+a2=（x﹣a）2，

    ∴a=，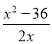

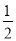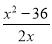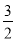    ∴y=3x﹣×6×=x+．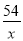

    综上所述，y=．

    【题型】解答题
    【结束】
    27

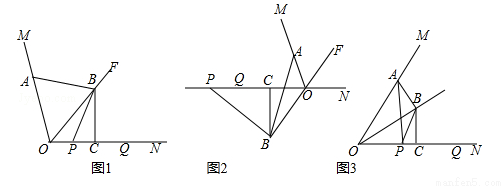
    （2017辽宁省抚顺市，第25题，12分）如图，OF是∠MON的平分线，点A在射线OM上，P，Q是直线ON上的两动点，点Q在点P的右侧，且PQ=OA，作线段OQ的垂直平分线，分别交直线OF、ON交于点B、点C，连接AB、PB．

    （1）如图1，当P、Q两点都在射线ON上时，请直接写出线段AB与PB的数量关系；

    （2）如图2，当P、Q两点都在射线ON的反向延长线上时，线段AB，PB是否还存在（1）中的数量关系？若存在，请写出证明过程；若不存在，请说明理由；

    （3）如图3，∠MON=60°，连接AP，设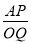=k，当P和Q两点都在射线ON上移动时，k是否存在最小值？若存在，请直接写出k的最小值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：江苏省东台市第七联盟2018届九年级上学期第三次质量检测数学试卷 题型：填空题

    二次函数y=ax2+bx+c图象上部分点的对应值如下表：

    x

    ﹣3

    ﹣2

    ﹣1

    0

    1

    2

    3

    4

    y

    6

    0

    ﹣4

    ﹣6

    ﹣6

    ﹣4

    0

    6

    则当y≤0时，x的取值范围为_________．

    查看答案和解析>>

    同步练习册答案