
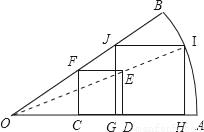
С������һ������ֽƬOAB����Ҫ����ֽƬ�Ͻ�һ�������Σ�ʹ������������ܴ�
С���ķ����ǣ���ͼ��������ֽƬOAB�ڣ���������CDEF��ʹC��D��OA�ϣ�F��OB�ϣ�����OE���ӳ�����AB��I����IH��ED��OA��H��IJ��OA��OB��J���ٻ�JG��FC��OA��G��
��1������ΪС���������ı���GHIJ��������������ǣ���֤����������ǣ���˵�����ɣ�
��2���������OAB��Բ�Ľǡ�AOB=30�㣬OA=6cm��С���صõ��ı���GHIJ����Ƕ��٣������ȷ��0.1cm����
��3����1����С���������ı���GHIJ����������Σ����ǰ����������ε��ڽ������Σ��ĸ�����ֱ������εİ뾶�ͻ��ϣ��������ٻ���һ�ֲ�ͬ��ͼ��1�������ε��ڽ������Σ�������ͼ�ۼ�����Ҫ��֤����

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ�����У�����У���� 2017-2018ѧ����꼶��һѧ�����в�����ѧ�Ծ� ���ͣ���ѡ��
�ө� ,0,
,0,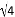 ,��,3.5��������У������ȡһ������鵽�������ĸ����ǣ�������
,��,3.5��������У������ȡһ������鵽�������ĸ����ǣ�������
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�걱ʦ�����꼶��ѧ�²� ��ĩ���� ���ͣ���ѡ��
��ͼ�����������ABCDE�У�����BE�����ABE�Ķ���Ϊ( )
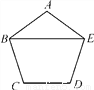
A. 30�� B. 36�� C. 54�� D. 72��
B ���������������ABCDE��������Σ� ��AB=AE����A=�� ���ABE=��AEB=. ��ѡB.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
�й��ġ�һ��һ·��ս�Ը����߹��Һ͵��������ܴ�ľ���Ч�棬����ij��������2016��������200��Ԫ��Ԥ��2018�������뽫�ﵽ1000��Ԫ����2016�굽2018��õ��������˾��������ƽ��������Ϊx,���з���Ϊ___________
���������������� ������ã� ���ʴ�Ϊ�� ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
һ�������Ĵ���װ�г���ɫ�����ͬ��5�������n���������������һ������������ĸ����� ����n�ǣ� ��
����n�ǣ� ��
A. 5 B. 8 C. 3 D. 13
C ���������������� ������ã� ����ã�n=3����ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ�����ж���ʵ��ѧУ2017���п���ѧģ���Ծ� ���ͣ������
ij�߿Ƽ���Ʒ������˾����Ա��50��������Ա�����¹���������±���
Ա�� | ������Ա | ��ͨ������Ա | |||||
��Ա�ṹ | �ܾ��� | ���ž��� | ������Ա | ������Ա | ������ | �м����� | ���ӹ� |
Ա���������� | 1 | 3 | 2 | 3 | 24 | 1 | |
ÿ���¹��ʣ�Ԫ�� | 21000 | 8400 | 2025 | 2200 | 1800 | 1600 | 950 |
��������������ݣ�����������⣺
��1���ù�˾�������������� ������
��2������Ա���¹��ʵ�ƽ����xΪ2500Ԫ����λ��Ϊ�� ��Ԫ������Ϊ�� ��Ԫ��
��3��С�ŵ���ҹ�˾ӦƸ��ͨ������Ա������ش���ͼ��С�ŵ����⣬��ָ���ã�2���е��ĸ�������С�Ž���Ա�����¹���ʵ��ˮƽ������Щ��
��4��ȥ���ĸ�������Ա�Ĺ��ʺ�������������Ա������ƽ������ ��������������������ж�
��������������������ж� �ܷ�ӳ�ù�˾Ա�����¹���ʵ��ˮƽ��
�ܷ�ӳ�ù�˾Ա�����¹���ʵ��ˮƽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ�����ж���ʵ��ѧУ2017���п���ѧģ���Ծ� ���ͣ������
�������⣺�ٶԶ�����ȣ��ڵ��������ε���������ȣ�����ֱ��ƽ�У�ͬλ����ȣ�����������Ϊ��������У��� �������������з����������ţ���
�ڢۣ� ����������ԭ�����������Ϊ:��ȵĽ��ǶԶ��ǣ�ԭ����Ϊ������,������Ϊ������; ��ԭ�����������Ϊ:����������ȵ��������ǵ��������Σ�ԭ����Ϊ������,������Ϊ������. ��ԭ�����������Ϊ:ͬλ�����,��ֱ��ƽ�У�ԭ����Ϊ������,������ҲΪ������. ��������Ϊ��������У��ڢ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�꽭��ʡ�������п���ѧһģ�Ծ� ���ͣ������
��ͼ��Rt��ABC�У���ACB=90�㣬AC=6cm��BC=8cm������P�ӵ�B��������BA������ÿ��5cm���ٶ����A�����˶���ͬʱ����Q�ӵ�C��������CB������ÿ��4cm���ٶ����B�����˶����˶�ʱ��Ϊt�루0��t��2��������PQ��
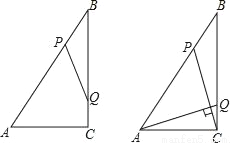
��1������BPQ���ABC���ƣ���t��ֵ��
��2������AQ��CP����AQ��CP����t��ֵ��
(1) t=1�� ;(2) ����������������� ��1���ɡ�B�ǡ�BPQ���ABC�Ĺ����ǣ���֪���������������ƣ���������������١�BPQ�ס�BAC���ڡ�BPQ�ס�BCA�������������������������ε����ʺ����⼴�ɽ�ö�Ӧ��t��ֵ�� ��2����ͼ1����P��PM��BC�ڵ�M��AQ��CP���ڵ�N���������֪����AQ��CPʱ����ACQ�ס�CMP�������������ε������г�����ʽ���ɽ�ö�Ӧ��t...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʡ�п���ѧ��ģ�Ծ� ���ͣ���ѡ��
���κ���y=ax2+bx+c(a��0)�Ĵ���ͼ����ͼ�����ڸö��κ���������˵���������( )
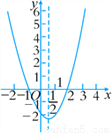
A. ��������Сֵ B. �Գ�����ֱ��x=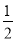
C. ��x<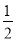 ʱ��y��x���������С D. ��-1<x<2ʱ��y>0
ʱ��y��x���������С D. ��-1<x<2ʱ��y>0
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com