
某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
员工 | 管理人员 | 普通工作人员 | |||||
人员结构 | 总经理 | 部门经理 | 科研人员 | 销售人员 | 高级技工 | 中级技工 | 勤杂工 |
员工数(名) | 1 | 3 | 2 | 3 | 24 | 1 | |
每人月工资(元) | 21000 | 8400 | 2025 | 2200 | 1800 | 1600 | 950 |
请你根据上述内容,解答下列问题:
(1)该公司“高级技工”有 名;
(2)所有员工月工资的平均数x为2500元,中位数为 元,众数为 元;
(3)小张到这家公司应聘普通工作人员.请你回答右图中小张的问题,并指出用(2)中的哪个数据向小张介绍员工的月工资实际水平更合理些;
(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资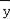 (结果保留整数),并判断
(结果保留整数),并判断 能否反映该公司员工的月工资实际水平.
能否反映该公司员工的月工资实际水平.

科目:初中数学 来源:2017年安徽省中考数学三模试卷 题型:解答题
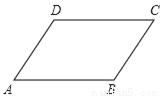
如图,已知平行四边形ABCD.
(1)用直尺和圆规作出么ABC的平分线BE,交AD的延长线于点E,交DC于点F(保留作图痕迹,不写作法);
(2)求证:△ABE是等腰三角形;
(3)在(1)中所得图形中,除△ABE外,请你写出其他的等腰三角形.(不要求证明)
查看答案和解析>>
科目:初中数学 来源:2017-2018学年北师大版八年级数学下册 期末测评 题型:单选题
观察出下列四种汽车标志,其中既是中心对称图形,又是轴对称图形的是( ).
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:辽宁省2018届九年级上学期期末考试数学试卷 题型:单选题
“赶陀螺”是一项深受人们喜爱的运动,如图所示是一个陀螺的立体结构图,已知底面圆的直径AB=6cm,圆柱体部分的高BC=5cm,圆锥体部分的高CD=4cm,则这个陀螺的表面积是( )
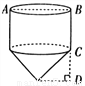
A. 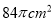 B.
B. 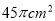
C. 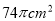 D.
D. 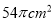
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市东海实验学校2017年中考数学模拟试卷 题型:解答题
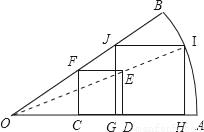
小明手上一张扇形纸片OAB.现要求在纸片上截一个正方形,使它的面积尽可能大.
小明的方案是:如图,在扇形纸片OAB内,画正方形CDEF,使C、D在OA上,F在OB上;连接OE并延长交弧AB于I,画IH∥ED交OA于H,IJ∥OA交OB于J,再画JG∥FC交OA于G.
(1)你认为小明画出的四边形GHIJ是正方形吗?如果是,请证明.如果不是,请说明理由.
(2)如果扇形OAB的圆心角∠AOB=30°,OA=6cm,小明截得的四边形GHIJ面积是多少(结果精确到0.1cm).
(3)(1)中小明画出的四边形GHIJ如果是正方形,我们把它叫做扇形的内接正方形(四个顶点分别在扇形的半径和弧上).请你再画出一种不同于图(1)的扇形的内接正方形(保留画图痕迹,不要求证明)
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市东海实验学校2017年中考数学模拟试卷 题型:填空题
如图,直线y=x与双曲线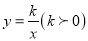 的一个交点为A,且OA=2,则k的值为 .
的一个交点为A,且OA=2,则k的值为 .
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市东海实验学校2017年中考数学模拟试卷 题型:单选题
下图是由10把相同的折扇组成的“蝶恋花”(图1)和梅花图案(图2)(图中的折扇无重叠),则梅花图案中的五角星的五个锐角均为( )
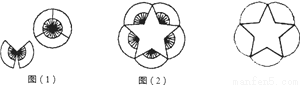
A. 36° B. 42° C. 45° D. 48°
D 【解析】试题分析:如图,梅花扇的内角的度数是:360°÷3=120°,180°﹣120°=60°,正五边形的每一个内角=(5﹣2)•180°÷5=108°,∴梅花图案中的五角星的五个锐角均为:108°﹣60°=48°.故选D.查看答案和解析>>
科目:初中数学 来源:2017年江苏省徐州市中考数学一模试卷 题型:解答题
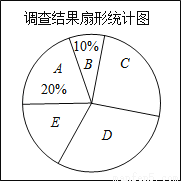
2014年全国两会民生话题成为社会焦点.合肥市记者为了了解百姓“两会民生话题”的聚焦点,随机调查了合肥市部分市民,并对调查结果进行整理.绘制了如图所示的不完整的统计图表.
组别 | 焦点话题 | 频数(人数) |
A | 食品安全 | 80 |
B | 教育医疗 | m |
C | 就业养老 | n |
D | 生态环保 | 120 |
E | 其他 | 60 |
请根据图表中提供的信息解答下列问题:
(1)填空:m= ,n= .扇形统计图中E组所占的百分比为 %;
(2)合肥市人口现有750万人,请你估计其中关注D组话题的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人关注C组话题的概率是多少?
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省中考数学二模试卷 题型:单选题
如图,按照三视图确定该几何体的全面积为(图中尺寸单位:cm)( )

A. 128πcm2 B. 160πcm2 C. 176πcm2 D. 192πcm2
D 【解析】∵几何体的主视图和左视图是相同的矩形,俯视图是圆, ∴该几何体为圆柱,且圆柱的高为20cm,底面直径为8cm, ∴圆柱的表面积为2×π×42+2π×4×20=32π+160π=192πcm2, 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com