练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列图形中，既是轴对称又是中心对称的图形是( )

    A. 正三角形 B. 平行四边形 C. 等腰梯形 D. 正方形

    D 【解析】A、正三角形是轴对称图形但不是中心对称图形； B、平行四边形是中心对称图形但不是轴对称图形； C、等腰梯形是轴对称图形，但不是轴对称图形； D、正方形既是轴对称图形也是中心对称图形； 故选D．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：内蒙古2018届九年级（上）期中数学试卷 题型：解答题

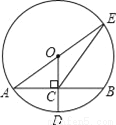
    如图，⊙O的半径OD⊥弦AB于点C，联结AO并延长交⊙O于点E，联结EC．已知AB=8，CD=2．

    （1）求OA的长度；

    （2）求CE的长度．

    （1）OA=5；（2）CE=2． 【解析】（1）【解析】 ∵在⊙O中，OD⊥弦AB，∴， ∵AB=8，∴AC=BC=4， 设OA为x，则OD=OA=x， ∵CD=2，∴OC=x﹣2 在Rt△ACO中，AC2+OC2=AO2 ∴42+（x﹣2）2=x2， 解得x=5， ∴OA=5； （2）【解析】 连接BE， ∵OA=OE，AC=BC，∴OC...

    查看答案和解析>>

    科目：初中数学 来源：江苏省盐城市阜宁县2018届九年级上学期期末考试数学试卷 题型：单选题

    如图，以点O为圆心的两个圆中，大圆的弦AB切小圆于点C，OA交小圆于.点D，若OD=2， tan∠OAB=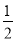，则AB的长是( )

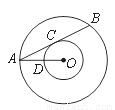
    A. 4 B. 2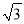 C. 8 D. 4

    C 【解析】试题解析：连接OC， ∵大圆的弦AB切小圆于点 C， ∴OC⊥AB， ∴AB=2AC， ∵OD=2， ∴OC=2， ∵tan∠OAB=， ∴AC=4， ∴AB=8， 故选C．

    查看答案和解析>>

    科目：初中数学 来源：四川省数学八年级下册期末复习测试卷 题型：填空题

    某校规定学生期末数学总评成绩由三部分构成：卷面成绩、课外论文成绩、平日表现成绩（三部分所占比例如图），若方方的三部分得分依次是92、80、84，则她这学期期末数学总评成绩是多少？

    88.8 【解析】试题分析：利用加权平均数的公式即可求出答案． 试题解析：由题意知，她这学期期末数学总评成绩=92×70%+80×20%+84×10%=88．8（分）．

    查看答案和解析>>

    科目：初中数学 来源：四川省数学八年级下册期末复习测试卷 题型：单选题

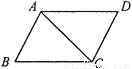
    如图，□ABCD的周长是28cm，△ABC的周长是22cm，则AC的长为（   ）

    A. 6cm B. 12cm C. 4cm D. 8cm

    D 【解析】∵?ABCD的周长是28cm， ∴AB+AD=14cm， ∵△ABC的周长是22cm， ∴AB+BC+AC=22cm， ∴AC=(AB+BC+AC)?(AB+AC)=22?14=8cm， 故选：D.

    查看答案和解析>>

    科目：初中数学 来源：2017年广东省佛山市中考数学模拟试卷（3） 题型：解答题

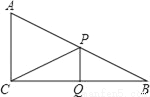
    已知Rt△ABC中，AC=5，BC=12，∠ACB=90°，P是AB边上的动点（与点A、B不重合），Q是BC边上的动点（与点B、C不重合）

    （1）如图，当PQ∥AC，且Q为BC的中点时，求线段CP的长；

    （2）当PQ与AC不平行时，△CPQ可能为直角三角形吗？若有可能，请求出线段CQ的长的取值范围；若不可能，请说明理由．

    （1）；（2）详见解析. 【解析】试题分析： （1）由题意易得AB=13，由Q是BC中点，PQ∥AC可得点P是AB中点，从而可得CP=AB=； （2）当AC与PQ不平行时，只有∠CPQ为直角，△CPQ才可能是直角三角形．根据圆中，直径所对的圆周角是直角，以CQ为直径作半圆D，当半圆D和直线AB有公共点时，点P运动到公共点处，∠PCQ就是直角；由此以CQ为直径作半圆D，当半圆D与A...

    查看答案和解析>>

    科目：初中数学 来源：2017年广东省佛山市中考数学模拟试卷（3） 题型：解答题

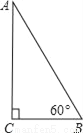
    有一个角是60°的直角三角形，求它的面积y与斜边x的函数关系式．

    y=． 【解析】试题分析： 由sinB=，cosB=，可得， ，再由S△ABC=AC·BC即可得到与间的函数关系式. 试题解析： ∵AB=x，∠B=60°，∠C=90°， ∴AC=AB×sin60°=x，BC=AB×cos60°=， 又∵S△ABC=AC·BC， ∴. 即与间的函数关系式为： .

    查看答案和解析>>

    科目：初中数学 来源：2017年广东省佛山市中考数学模拟试卷（3） 题型：单选题

    如果零上3℃记作+3℃，那么零下6℃记作（　　）

    A. 6℃ B. ﹣6℃ C. 6 D. ﹣6

    B 【解析】∵“零上”和“零下”的意义相反。 ∴当零上3℃记作+3℃时，零下6℃应记作-6℃. 故选B.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年江苏省苏州市初三上期中模拟数学试卷 题型：解答题

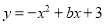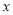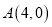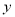    如图，二次函数的图象与轴的一个交点为，与轴交于点．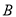

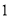    （）求此二次函数关系式和点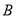的坐标．

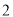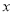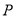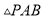    （）在轴的正半轴上是否存在一点，使得是以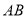为底的等腰三角形？若存在，求出点的坐标．若不存在，请说明理由．

    （）（） 【解析】试题分析： （1）把点A的坐标代入二次函数，求出b的值，确定二次函数关系式，把x=0代入二次函数求出点B的坐标．（2）当BP=AP时，在直角△OBP中，根据勾股定理列出方程，解方程求得x的值，即可得点P的坐标． 试题解析： （）把代入得： ． ∴， 令， ． ∴． （） 设． ∵为底， ∴． ∴ OP=...

    查看答案和解析>>

    同步练习册答案