
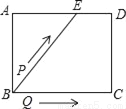
如图,矩形ABCD中,AB=4cm,AD=5cm,点E在AD上,且AE=3cm,点P、Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s,设P、Q出发t秒,△BPQ的面积为y cm2.则y与t的函数关系图象大致是( )
A. 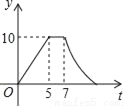 B.
B. 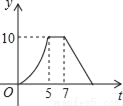 C.
C. 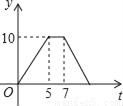 D.
D. 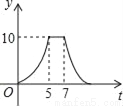
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:山东省寿光市2017-2018学年七年级上期末模拟数学试卷 题型:填空题
如图所示的图形绕虚线旋转一周得到的几何体的名称是________.
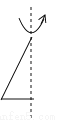
查看答案和解析>>
科目:初中数学 来源:2017年吉林省中考数学一诊试卷 题型:填空题
如图,△ABC中,∠C=90°,AC=6,BC=8,动点P从A点出发,以1cm/s的速度,沿A﹣C﹣B向B点运动,同时,动点Q从C点出发,以2cm/s的速度,沿C﹣B﹣A向A点运动,当其中一点运动到终点时,两点同时停止运动.设运动时间为t秒,当t=_____秒时,△PCQ的面积等于8cm2.
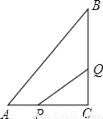
查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:解答题
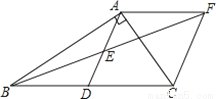
在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=3,AB=4,求菱形ADCF的面积.
查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:填空题
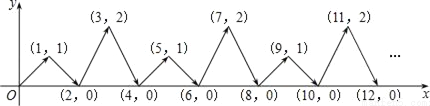
如图,动点P在平面直角坐标系中按图中箭头所示的方向运动,第1次从原点运动到(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过2017次运动后,动点P的坐标为_____.
查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:单选题
济南某中学足球队的18名队员的年龄如表所示:
年龄(单位:岁) |
| 12 |
| 13 |
| 14 |
| 15 |
人数 |
| 3 |
| 5 |
| 6 |
| 4 |
这18名队员年龄的众数和中位数分别是( )
A.13岁,14岁 B.14岁,14岁 C.14岁,13岁 D.14岁,15岁
B 【解析】试题分析:∵济南某中学足球队的18名队员中,14岁的最多,有6人, ∴这18名队员年龄的众数是14岁; ∵18÷2=9,第9名和第10名的成绩是中间两个数, ∵这组数据的中间两个数分别是14岁、14岁, ∴这18名队员年龄的中位数是:(14+14)÷2=28÷2=14(岁) 综上,可得这18名队员年龄的众数是14岁,中位数是14岁. 故选:B....查看答案和解析>>
科目:初中数学 来源:2017年吉林省长春市中考数学模拟试卷(7) 题型:解答题
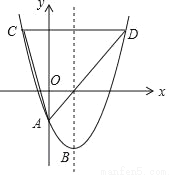
如图,在平面直角坐标系中,抛物线y=a(x﹣2)2﹣4与y轴交于点A,顶点为B,点A的坐标为(0,﹣2),点C在抛物线上(不与点A,B重合),过点C作y轴的垂线交抛物线于点D,连结AC,AD,CD,设点C的横坐标为m.
(1)求这条抛物线所对应的函数表达式.
(2)用含m的代数式表示线段CD的长.
(3)点E是抛物线对称轴上一点,且点E的纵坐标比点C的纵坐标小1,连结BD,DE,设△ACD的面积为S1,△BDE的面积为S2,且S1•S2≠0,求S2=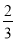 S1时m的值.
S1时m的值.
(4)将抛物线y=a(x﹣2)2﹣4沿x=2平移,得到抛物线y=a(x﹣2)2+k,过点C作y轴平行线与抛物线y=a(x﹣2)2+k交于点F,若CD与y轴交于点G,且CD=6,直接写出使AC=FG的点F的坐标.
查看答案和解析>>
科目:初中数学 来源:2017年吉林省长春市中考数学模拟试卷(7) 题型:单选题
如图,A,B,C为⊙O上三点,若∠ACB=20°,则∠BAO的大小为( )
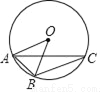
A. 40° B. 60° C. 70° D. 80°
C 【解析】∵∠ACB=20°, ∴∠AOB=2×20°=40°, ∵AO=BO, ∴∠BAO=∠OBA=(180°?40°)÷2=70°, 故选:C.查看答案和解析>>
科目:初中数学 来源:湖北省武汉市汉阳区2018届九年级(上)期中数学试卷(解析版) 题型:填空题
如图,用篱笆靠墙围成矩形花圃ABCD,墙可利用的最大长度为15m,一面利用旧墙,其余三面用篱笆围,篱笆长为24m,若围成的花圃面积为40m2时,平行于墙的BC边长为_____m.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com