
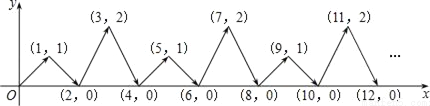
如图,动点P在平面直角坐标系中按图中箭头所示的方向运动,第1次从原点运动到(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过2017次运动后,动点P的坐标为_____.
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源:山东省寿光市2017-2018学年七年级上期末模拟数学试卷 题型:填空题
点A在数轴上所表示的数为﹣1,若AB=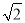 ,则点B在数轴上所表示的数为________.
,则点B在数轴上所表示的数为________.
查看答案和解析>>
科目:初中数学 来源:2017年吉林省中考数学一诊试卷 题型:解答题
已知关于x的一元二次方程x2﹣2(m+1)x+m2+2=0
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根分别为x1、x2,且满足x12+x22=10,求实数m的值.
(1)m≥(2)实数m的值为1. 【解析】试题分析:(1)根据方程的系数结合根的判别式即可得出关于m的一元一次不等式,解之即可得出结论; (2)根据根与系数的关系即可得出x1+x2=2(m+1)、x1•x2=m2+2,结合x12+x22=10即可得出关于m的一元二次方程,解之即可得出m的值,再结合(1)的结论即可得出结论. 试题解析:(1)∵方程x2﹣2(m+1)x+m2+2=0...查看答案和解析>>
科目:初中数学 来源:2017年吉林省中考数学一诊试卷 题型:单选题
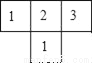
如图是由几个大小相同的小正方体搭成的几何体的俯视图,小正方形中数字表示该位置小正方体的个数,则该几何体的左视图是( )
A.  B.
B. 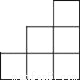 C.
C.  D.
D. 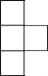
查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:解答题
如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C.
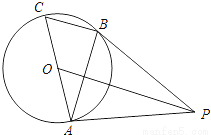
(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为2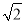 ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:单选题
如图,矩形ABCD中,AB=4cm,AD=5cm,点E在AD上,且AE=3cm,点P、Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s,设P、Q出发t秒,△BPQ的面积为y cm2.则y与t的函数关系图象大致是( )
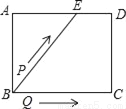
A. 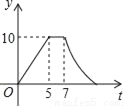 B.
B. 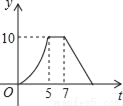 C.
C. 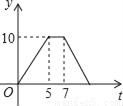 D.
D. 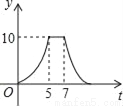
查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:单选题
下列运算正确的是( )
A.a2+a3=a5 B.a2•a3=a6 C.(a2b3)3=a5b6 D.(a2)3=a6
D. 【解析】 试题解析:A、a2与a3不是同类项不能合并,故本选项错误; B、应为a2•a3=a5,故本选项错误; C、应为(a2b3)3=a6b9,故本选项错误; D、(a2)3=a6,正确; 故选D.查看答案和解析>>
科目:初中数学 来源:2017年吉林省长春市中考数学模拟试卷(7) 题型:填空题
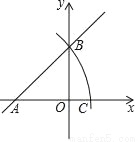
如图,在平面直角坐标系中,直线y=x+b交x轴于点A,交y轴于点B,以点A为圆心,线段AB长为半径作圆弧,交x轴正半轴于点C,若AC=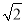 ,则b的值为_____.
,则b的值为_____.
查看答案和解析>>
科目:初中数学 来源:湖北省武汉市汉阳区2018届九年级(上)期中数学试卷(解析版) 题型:解答题
关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1,x2.
(1)求实数k的取值范围;
(2)若方程两实根x1,x2满足|x1|+|x2|=x1·x2,求k的值.
(1) k>;(2)k=2 【解析】试题分析:(1)根据根与系数的关系得出△>0,代入求出即可; (2)根据根与系数的关系得出x1+x2=﹣(2k+1),x1•x2=k2+1,根据x1+x2=﹣x1•x2得出﹣(2k+1)=﹣(k2+1),求出方程的解,再根据(1)的范围确定即可. 试题解析:(1)∵原方程有两个不相等的实数根, ∴△=(2k+1)2﹣4(k2+1)>0, ...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com