
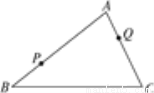
如图所示,P,Q为△ABC边上的两个定点,在BC上求作一点R,使△PQR的周长最小.
科目:初中数学 来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质 题型:填空题
矩形是轴对称图形,对角线是它的对称轴.( )
× 【解析】矩形是轴对称图形,对边中点连线所在的直线是它的对称轴,对角线不是它的对称轴, 故原语句是错误的.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(3)练习 题型:填空题
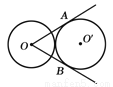
如图10,两个等圆⊙O与⊙O′外切,过点O作⊙O′的两条切线OA、OB,A、B是切点,则∠AOB=_________.
查看答案和解析>>
科目:初中数学 来源:人教版八年级上册 第十二章 全等三角形 12.2 三角形全等的判定 同步练习题 含答案 题型:填空题
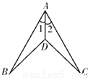
如图,∠1=∠2,由AAS判定△ABD≌△ACD,则需添加的条件是_______.
查看答案和解析>>
科目:初中数学 来源:人教版八年级上册 第十二章 全等三角形 12.2 三角形全等的判定 同步练习题 含答案 题型:单选题
如图,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是( )
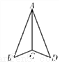
A. 120° B. 125° C. 127° D. 104°
C 【解析】试题分析:AB=AD,CB=CD,AC=AC所以∆ABC?∆ACD,所以∠B=∠D=30°,因为∠BAD=46°,所以∠CAD=23°,所以∠ACD=180°-30°-23°=127°,故选C.查看答案和解析>>
科目:初中数学 来源:新人教版数学八年级上册第十三章轴对称13.1.2《线段的垂直平分线的性质》课时练习 题型:
如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.
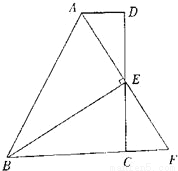
查看答案和解析>>
科目:初中数学 来源:新人教版数学八年级上册第十三章轴对称13.1.2《线段的垂直平分线的性质》课时练习 题型:
如图,∠ABC=50°,AD垂直且平分BC于点D,∠ABC的平分线BE交AD于点E,连接EC,则∠AEC的度数是( )
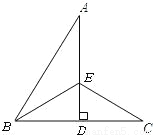
A. 50° B. 25° C. 80° D. 115°
D 【解析】因为AD垂直且平分BC,所以EB=EC,所以∠EBC=∠C. 因为BE平分∠ABC,所以∠ABC=2∠EBC=50°,所以∠EBC=25°,所以∠C=25°. 所以∠AEC=∠C+∠EDC=25°+90°=115°. 故选D.查看答案和解析>>
科目:初中数学 来源:安徽省濉溪县2017-2018学年七年级上学期期中考试数学试卷 题型:解答题
阅读下面的解题过程:
解方程:|x+3|=2.
【解析】
当x+3≥0时,原方程可化成为x+3=2
解得x=-1,经检验x=-1是方程的解;
当x+3<0,原方程可化为,-(x+3)=2
解得x=-5,经检验x=-5是方程的解.
所以原方程的解是x=-1,x=-5.
解答下面的两个问题:
(1)解方程:|3x-2|-4=0;
探究:当值a为何值时,方程|x-2|=a, ①无解;②只有一个解;③有两个解.
(1)x=2或x=-; (2) a小于0,无解;a=0,一个解;a大于0,两个解. 【解析】试题分析:(1)根据绝对值的性质,可化简绝对值,根据解方程,可得答案; (2)根据绝对值的性质,可得答案. 【解析】 (1)当3x﹣2≥0时,原方程可化为3x﹣2=4, 解得x=2,经检验x=2是方程的解; 当3x﹣2<0时,原方程可化为﹣(3x﹣2)=4, 解得x=﹣...查看答案和解析>>
科目:初中数学 来源:2017北师大版数学八年级上册 第4章 一次函数 单元检测题 题型:单选题
关于的一次函数y=kx+k2+1的图象可能是( )
A. 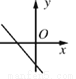 B.
B. 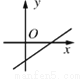 C.
C. 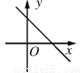 D.
D. 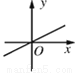
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com