
如果菱形的两条对角线的长为a和b,且a,b满足(a-1)2+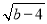 =0,那么菱形的面积等于 .
=0,那么菱形的面积等于 .
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源:江苏省2017-2018学年七年级12月月考数学试卷 题型:单选题
如图,数轴上有A、B、C、D四个整数点(即各点均表示整数),且3AB=BC=2CD.若A、D两点所表示的数分别是﹣6和5,则线段AC的中点所表示的数是( )

A. ﹣3 B. ﹣1 C. 3 D. ﹣2
D 【解析】首先设BC为6x,根据3AB=BC=2CD表示出AB=2x,CD=3x,然后根据线段AD的长度建立方程,进而求出点C所表示的数,再利用两点之间的中点公式即可得出答案. 【解析】 设BC=6x, ∵3AB=BC=2CD, ∴AB=2x,CD=3x, ∴AD=AB+BC+CD=11x, ∵A,D两点所表示的数分别是?6和5, ∴AD=11, ...查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级上学期第二次月考数学试卷 题型:填空题
如图,在⊙O中,AB为直径,C、D为⊙O上两点,若∠C=25°,则∠ABD=_____.
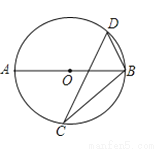
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(人教版):期末检测题(二) 题型:解答题
某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的原始分均为100分.前6名选手的得分如下:
序号 项目 | 1 | 2 | 3 | 4 | 5 | 6 |
笔试成绩/分 | 85 | 92 | 84 | 90 | 84 | 80 |
面试成绩/分 | 90 | 88 | 86 | 90 | 80 | 85 |
根据规定,笔试成绩和面试成绩分别按一定的百分比折合成综合成绩(综合成绩的满分仍为100分).
(1)这6名选手笔试成绩的中位数是________分,众数是________分;
(2)现得知1号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比;
(3)求出其余五名选手的综合成绩,并以综合成绩排序确定前两名人选.
(1)84.5,84; (2)笔试成绩和面试成绩所占的百分比分别是40%,60%; (3)综合成绩排序前两名的人选是4号和2号选手. 【解析】试题分析:(1)根据中位数和众数的定义即把这组数据从小到大排列,再找出最中间两个数的平均数就是中位数,再找出出现的次数最多的数即是众数; (2)先设笔试成绩和面试成绩各占的百分百是x,y,根据题意列出方程组,求出x,y的值即可; ...查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(人教版):期末检测题(二) 题型:填空题
如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=4.设AB=x,AD=y,则x2+(y﹣4)2的值为 .
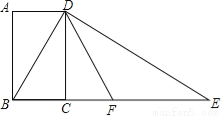
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(人教版):期末检测题(二) 题型:单选题
某移动通讯公司提供了A,B两种方案的通讯费用y(元)与通话时间x(分)之间的关系,如图所示,则以下说法错误的是( )
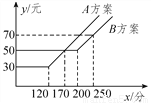
A. 若通话时间少于120分,则A方案比B方案便宜20元
B. 若通话时间超过200分,则B方案比A方案便宜12元
C. 若通讯费用为60元,则B方案比A方案的通话时间多
D. 若两种方案通讯费用相差10元,则通话时间是145分或185分
D 【解析】从图象可以看出通话时间少于120 分钟,则B 方案比A 方案便宜 20元,故 A正确; 由图象可以求得方案 A的解析表达式为y= ,方案 B的解析表达式为y=,所以通话时间超过 200分钟,则B 方案比 A方案便宜12 元,故 B正确; 由y=60 作x 轴的平行线,从图象看出当通信费用为60 元时,则 B方案比 A方案的通话时间多,故 C正确;两种方案通信费用相差1...查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学下册(华师大版):期末检测2 题型:解答题
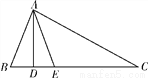
如图,在△ABC中,AD⊥BC,AE平分∠BAC.
(1)若∠B=72°,∠C=30°,①求∠BAE的度数;②求∠DAE的度数;
(2)探究:如果只知道∠B=∠C+42°,也能求出∠DAE的度数吗?若能,请你写出求解过程;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学下册(华师大版):期末检测2 题型:单选题
已知关于x、y的方程组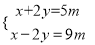 的解满足3x+2y=19,则m的值为( )
的解满足3x+2y=19,则m的值为( )
A. 1 B. 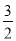 C. 5 D. 7
C. 5 D. 7
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2017-2018学年九年级上学期期末考试数学试卷 题型:解答题
解方程:
(1)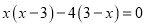 ; (2)
; (2)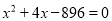 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com