
将分式方程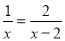 去分母后得到的整式方程正确的是( )
去分母后得到的整式方程正确的是( )
A. x-2=2x B. x2-2x=2x
C. x-2=x D. x=2x-4
A 【解析】方程两边同时乘以x(x-2)得 x-2=2x, 故选A.科目:初中数学 来源:2017-2018学年七年级数学人教版上册:第1、2章单元测试卷 题型:填空题
已知多项式x|m|+(m-2)x-10是二次三项式,m为常数,则m的值为____.
-2 【解析】因为多项式x|m|+(m-2)x-10是二次三项式, 可得:m?2≠0,|m|=2, 解得:m=?2, 故答案为:?2查看答案和解析>>
科目:初中数学 来源:山东省临沂市经济开发区2018届九年级上学期期末考试数学试卷 题型:单选题
如图,点P在等边△ABC的内部,且PC=6,PA=8,PB=10,将线段PC绕点C顺时针旋转60°得到P'C,连接AP',则cos∠PAP'的值为等于( )
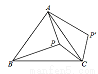
A. 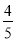 B.
B. 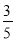 C.
C. 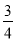 D.
D. 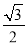
查看答案和解析>>
科目:初中数学 来源:2018届中考数学一轮复习单元检测:第6讲 分式方程及其应用 题型:单选题
解分式方程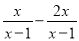 =1,可知方程的解为( )
=1,可知方程的解为( )
A. x=1 B. x=3 C. x=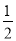 D. 无解
D. 无解
查看答案和解析>>
科目:初中数学 来源:2018届中考数学一轮复习单元检测:第6讲 分式方程及其应用 题型:单选题
电动车每小时比自行车多行驶了25千米,自行车行驶30千米比电动车行驶40千米多用了1小时,求两车的平均速度各为多少?设自行车的平均速度为x千米/小时,应列方程为( )
A. 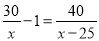 B.
B. 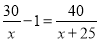
C. 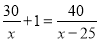 D.
D. 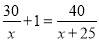
查看答案和解析>>
科目:初中数学 来源:广西北海市银海区2017年秋季学期教学质量监测七年级数学试卷 题型:解答题
综合题:先化简,再求值
(1)先化简,再求值:x 2 -(x+2)(2-x)-2(x-5) 2 , 其中x=3.
(2)解不等式组  ,并求它的整数解.
,并求它的整数解.
查看答案和解析>>
科目:初中数学 来源:广西北海市银海区2017年秋季学期教学质量监测七年级数学试卷 题型:单选题
将如图所示的两个平面图形绕轴旋转一周,对其所得的立体图形,下列说法正确的是( )
主视图相同 B.左视图相同 C.俯视图相同 D.三种视图都不相同

查看答案和解析>>
科目:初中数学 来源:人教版九年级下册数学 第26章 反比例函数 单元检测卷 题型:填空题
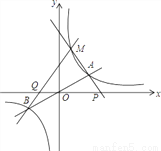
如图,已知双曲线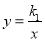 与直线y=k2x(k1,k2都为常数)相交于A,B两点,在第一象限内双曲线
与直线y=k2x(k1,k2都为常数)相交于A,B两点,在第一象限内双曲线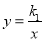 上有一点M(M在A的左侧),设直线MA,MB分别与x轴交于P,Q两点,若MA=m•AP,MB=n•QB,则n﹣m的值是________.
上有一点M(M在A的左侧),设直线MA,MB分别与x轴交于P,Q两点,若MA=m•AP,MB=n•QB,则n﹣m的值是________.
查看答案和解析>>
科目:初中数学 来源:人教版九年级下册数学 第27章 相似 单元检测卷 题型:解答题
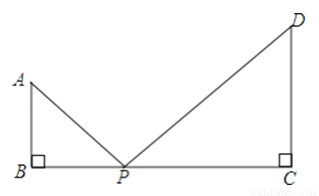
已知:AB⊥BC于B,CD⊥BC于C,AB=4,CD=6,BC=14,点P在BD上移动,当以P,C,D为顶点的三角形与△ABP相似时,求PB的长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com