练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

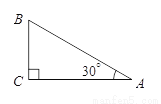
    如图 ，在Rt△ABC中，∠C=90°，∠A=30°，AC=3，则斜边AB=______．

    2 【解析】∵∠C=90°，∠A=30°，∴AB=2BC，AB2=BC2+AC2 ,又∵AC=3，∴AB=2 .
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：浙江省宁波市鄞州区九校2017-2018学年八年级上册数学第一次月考试卷 题型：单选题

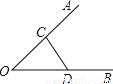
    如图，在CD上求一点P，使它到OA，OB的距离相等，则P点是（ ）

    A. 线段CD的中点 B. OA与OB的中垂线的交点

    C. OA与CD的中垂线的交点 D. CD与∠AOB的平分线的交点

    D 【解析】试题分析：利用角的平分线上的点到角的两边的距离相等可知CD与∠AOB的平分线的交P． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2017-2018学年八年级（上）期中数学试卷 题型：填空题

    已知点P到x轴，y轴的距离分别是2和3，且点P关于y轴对称的点在第四象限，则点P的坐标是_____．

    （﹣3，﹣2） 【解析】由题， 点P关于y轴对称的点在第四象限，则点P在第三象限，又因为点P到x轴、y轴的距离分别是2和3，所以P(-3，-2). 试题分析：点到x轴的距离是其纵坐标，到y轴的距离是其横坐标，由题， 点P关于y轴对称的点在第四象限，则点P在第三象限，又因为点P到x轴、y轴的距离分别是2和3，所以P(-3，-2).

    查看答案和解析>>

    科目：初中数学 来源：湖北省黄冈市2017-2018学年八年级（上）期中数学试 题型：解答题

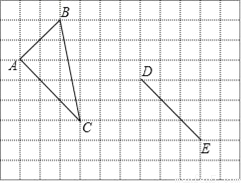
    如图所示的网格中有△ABC．

    （1）试在DE一侧找出格点C，使得以D，E，C为顶点的三角形与△ABC全等；

    （2）计算△ABC的面积．

    （1）见解析；（2）3.5． 【解析】试题解析：试题分析： 直接利用网格，结合全等三角形的判定方法得出符合题意得方程. 用所在矩形的面积减去三个直角三角形的面积即可. 试题解析：（1）如图所示，格点即为所求； （2）的面积

    查看答案和解析>>

    科目：初中数学 来源：湖北省黄冈市2017-2018学年八年级（上）期中数学试 题型：填空题

    如图,正三角形网格中,已有两个小正三角形被涂黑,再将图中其余小正三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形的方法有______种.

    3 【解析】试题分析：根据轴对称的概念作答．如果一个图形沿一条直线对折，直线两旁的部分能互相重合，那么这个图形叫做轴对称图形． 【解析】 选择小正三角形涂黑，使整个被涂黑的图案构成一个轴对称图形， 选择的位置有以下几种：1处，2处，3处，选择的位置共有3处． 故答案为：3．

    查看答案和解析>>

    科目：初中数学 来源：湖北省黄冈市2017-2018学年八年级（上）期中数学试 题型：单选题

    如图，在Rt△ABC的斜边BC上截取CD=CA，过点D作DE⊥BC交AB于点E，则有（　　）

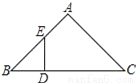
    A. DE=DB B. DE=AE C. AE=BE D. AE=BD

    B 【解析】试题解析：连接 在和中， ∴≌（HL）， 故B选项正确； 在中， ，即，故C选项错误； 根据已知不能得出，故A选项错误； 根据已知不能得出，由，即不能推出，故D选项错误． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：广东省汕头市潮南区两英镇2018届九年级上学期期末质检数学试卷 题型：解答题

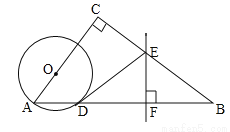
    如图，在△ABC中，∠C=90°，点O在AC上，以OA为半径的⊙O交AB于点D，BD的垂直平分线交BC于点E，交BD于点F，连接DE．

    （1）判断直线DE与⊙O的位置关系，并说明理由；

    （2）若AC=6，BC=8，OA=2，求线段DE的长．

    （1）直线DE与⊙O相切；（2）4.75． 【解析】试题分析：（1）连接OD，通过线段垂直平分线的性质和等腰三角形的性质证明∠EDB＋∠ODA＝90°，进而得出OD⊥DE，根据切线的判定即可得出结论； （2）连接OE，作OH⊥AD于H．则AH＝DH，由△AOH∽△ABC，可得，推出AH＝，AD＝，设DE＝BE＝x，CE＝8－x，根据OE2＝DE2＋OD2＝EC2＋OC2，列出方程即可解...

    查看答案和解析>>

    科目：初中数学 来源：广东省汕头市潮南区两英镇2018届九年级上学期期末质检数学试卷 题型：单选题

    已知点A（1，a）、点B（b，2）关于原点对称，则a+b的值为（　　）

    A. ﹣3 B. 3 C. ﹣1 D. 1

    A 【解析】【解析】 ∵点A（1，a）、点B（b，2）关于原点对称，∴b=﹣1，a=﹣2，a+b=﹣3，故选A．

    查看答案和解析>>

    科目：初中数学 来源：北京市2018届九年级（上）期中数学试卷 题型：填空题

    已知关于x的二次函数y=ax2+（a2﹣1）x﹣a的图象与x轴的一个交点的坐标为（m，0），若3＜m＜4，则a的取值范围是_____．

    ＜a＜或﹣4＜a＜﹣3 【解析】∵y=ax2+（a2﹣1）x﹣a=（ax﹣1）（x+a）， ∴当y=0时，可解得：x1=，x2=﹣a， ∴抛物线与x轴的交点为（，0）和（﹣a，0）． ∵抛物线与x轴的一个交点的坐标为（m，0）且2＜m＜3， ∴（1）当a＞0时，3＜＜4，解得； （2）当a＜0时，3＜﹣a＜4，解得﹣4＜a＜﹣3． 综上所述，a的取值范围是...

    查看答案和解析>>

    同步练习册答案