
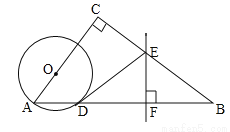
��ͼ���ڡ�ABC�У���C=90�㣬��O��AC�ϣ���OAΪ�뾶�ġ�O��AB�ڵ�D��BD�Ĵ�ֱƽ���߽�BC�ڵ�E����BD�ڵ�F������DE��
��1���ж�ֱ��DE���O��λ�ù�ϵ����˵�����ɣ�
��2����AC=6��BC=8��OA=2�����߶�DE�ij���
 ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д�
ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д� ���������ν�ϵ�д�
���������ν�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016-2017ѧ��ӱ�ʡ�żҿ����Ŷ������꼶���£���ĩ��ѧ�Ծ� ���ͣ������
��ʵ��m��n ����|m��2|+��n��2014��2=0����m��1+n0=______��
. ��������|m��2|+��n��2014��2=0�� m��2=0��n��2014=0�� m =2��n=2014�� m��1+n0=2��1+20140=+1=�� �ʴ�Ϊ�� ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
�㣨3��2������y��ԳƵ�Ϊ��������
A. ����3��2�� B. ��3����2�� C. ��2����3�� D. ��3����2��
A ��������ƽ��ֱ������ϵ������һ��P��x��y��������y��ĶԳƵ�������ǣ���x��y��������������ĶԳƵ㣬�����겻�䣬���������෴���� �㣨3��2������y��ԳƵ�Ϊ������3��2���� ��ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�Ƹ���2017-2018ѧ����꼶���ϣ�������ѧ�� ���ͣ������
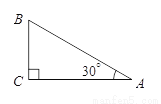
��ͼ ����Rt��ABC�У���C=90�㣬��A=30�㣬AC=3����б��AB=______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�Ƹ���2017-2018ѧ����꼶���ϣ�������ѧ�� ���ͣ���ѡ��
��ͼ����ABC�ա�ADE�������н��۴�����ǣ�������
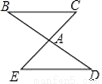
A. ��B=��D B. DE=CB C. ��BAC=��DAE D. AB=AE
D ������������������ߡ� ��ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ��ͷ�г�������Ӣ��2018����꼶��ѧ����ĩ�ʼ���ѧ�Ծ� ���ͣ������
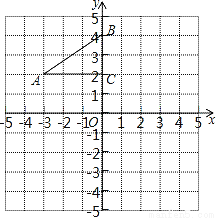
��ͼ����ƽ��ֱ������ϵ�У�Rt��ABC����������ֱ���A����3��2����B��0��4����C��0��2��������ABC�Ե�CΪ��ת������ת180�㣬������ת���Ӧ�ġ�A1B1C1����д��A1��B1�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ��ͷ�г�������Ӣ��2018����꼶��ѧ����ĩ�ʼ���ѧ�Ծ� ���ͣ������
�����κ���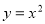 ��ͼ����x������ƽ��2����λ����ƽ�ƺ�������߶�Ӧ�Ķ��κ����ı���ʽΪ ��
��ͼ����x������ƽ��2����λ����ƽ�ƺ�������߶�Ӧ�Ķ��κ����ı���ʽΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ�����꼶��ѧ�ڵڶ����¿���ѧ�Ծ� ���ͣ������
��֪����6x��9��10x��45�뷽��3a��1��3��x��a����2a�Ľ���ͬ
��1���������ͬ�Ľ⣻
��2����a��ֵ��
��3����[m]��ʾ������m�������������[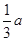 ��2]��ֵ
��2]��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������2018����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
����̨Ԥ�⡰���н���ĸ�����90%������Ԥ�����ȷ�����ǣ�������
A. �������콫��90%�ĵ������� B. �������콫��90%��ʱ�併��
C. ������в�����߿϶������� D. ������в�����߿��ܻ�����
D �������������н���ĸ�����90%������˵�������귢���Ŀ����Ժܴ���һ����һ���ᷢ��������A��B��C����ѡ���е�˵��������ȷ��ֻ��D�������⣮ ��ѡD���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com