
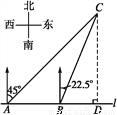
��ͼ,�ڱ�ֱ�ĺ�����l����A,B�����۲�վ,AB=2 km,��A����ô�C�ڱ�ƫ��45��ķ���,��B����ô�C�ڱ�ƫ��22.5��ķ���,��C�뺣����l�ľ���(��CD�ij�)Ϊ(����)
A. 4 km B. 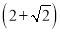 km C. 2
km C. 2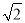 km D.
km D. 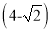 km
km
 ��˼άС�ھ�100����ҵ��ϵ�д�
��˼άС�ھ�100����ҵ��ϵ�д� ��ʦָ��һ��ͨϵ�д�
��ʦָ��һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���Ĵ�ʡ������2018����꼶��ѧ�ڽ�ѧˮƽ�����ѧ�Ծ� ���ͣ������
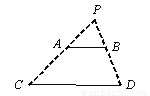
��ͼ�����P�ں��AB���Ϸ���AB�ڵƹ��µ�Ӱ��ΪCD��AB��CD��AB��2m��CD��6m����P��CD�ľ�����3m����P�� AB�ľ�����__________m��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������У2017-2018ѧ�����꼶��ѧ�ڵڶ��ο�����ѧ�Ծ� ���ͣ���ѡ��
��֪����ʽ12x��24�� -4��2x��ֵ��Ϊ�෴������ôx��ֵ����( )
A. ��2 B. ��1 C. 1 D. 2
D ��������������ã�12x-24+(-4+2x)=0�� ��ã�x=2�� ��ѡD.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018����ѧ��ʦ�����꼶��ѧ�²����в����Ծ� ���ͣ���ѡ��
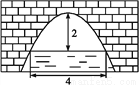
��ͼ��һ�������Ϊ��������״�Ĺ���,��ˮ���4 mʱ,����(���Ŷ�����ߵ�)��ˮ��2 m,��ˮ���½�1 mʱ,ˮ��Ŀ���Ϊ_____m.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018����ѧ��ʦ�����꼶��ѧ�²����в����Ծ� ���ͣ���ѡ��
ij�㳡�и���������Ȫ,����һ����ˮ����ˮ�����߶�Ϊ3 m,��ʱ����ˮ�ܵ�ˮƽ����Ϊ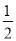 m,����ͼ��ƽ��ֱ������ϵ��,�����Ȫ�ĺ�������ʽ��(����)
m,����ͼ��ƽ��ֱ������ϵ��,�����Ȫ�ĺ�������ʽ��(����)
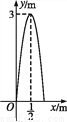
A. y=-3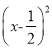 +3 B. y=-3
+3 B. y=-3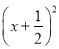 +3 C. y=-12
+3 C. y=-12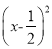 +3 D. y=-12
+3 D. y=-12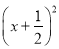 +3
+3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����꼶��ѧ�²ᣨ�˽̰棩��ĩ����� ���ͣ������
��2017�㽭ʡ̨���У���ͥ����ҩƷ���ڡ�����Σ�շ����������������Ⱦ������Σ��������ij��ҩ�ಿ��Ϊ�˽������ͥ��������ҩƷ�ķ�ʽ��������ȫ�м�ͥ��һ�μ�����������ˣ�
��1������ѡȡ�����ķ����������һ���� ����ֻ��������ȷ�𰸵���ţ�
����������ij���������Լ�ͥΪ��λ�����ȡ������ȫ��ҽ���������Լ�ͥΪ��λ�����ȡ������ȫ�г�ס�˿����Լ�ͥΪ��λ�����ȡ��
��2�����γ������˷��֣����ܵ��˵ļ�ͥ���й���ҩƷ���ֽ��й����ݳ�����ͼ��
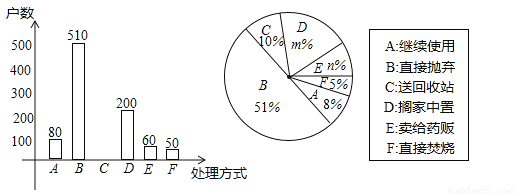
��m= ��n= ��
�ڲ�ȫ����ͳ��ͼ��
�۸��ݵ������ݣ�����Ϊ���������ͥ��������ҩƷ����ķ�ʽ��ʲô��
�ܼ�ͥ����ҩƷ����ȷ������ʽ���ͻ��յ㣬��������180��ͥ������ƴ�Լ�ж��ٻ���ͥ��������ҩƷ�ķ�ʽ���ͻ��յ㣮
��1���ۣ���2����20��6������ͼ����������B�ࣻ��18�� �������������������1�����ݼ���������Ķ��弴�ɵó���. ��2��������ɵó��ܻ���Ϊ1000�����Ӷ����m��n��ֵ. �ڸ������ݿ����C�Ļ������Ӷ���ȫ����ͳ��ͼ. �۸��ݵ������ݣ������������������֪�����������ͥ��������ҩƷ�����ʽ��ֱ�Ӷ���. �ܸ��������������壬��������ͻ��յ�ļ�ͥ����. ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����꼶��ѧ�²ᣨ�˽̰棩��ĩ����� ���ͣ������
����ʽ�� ����������______��
����������______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�人�к�ɽ��2018����꼶���ϣ�������ѧ�Ծ� ���ͣ������
Ϊ������������ѧУ������ͼ��ʾ�ľ���ABCD�յ��Ͻ����̻����滮���м��һ���ı���MNQP���ֻ���������Ŀ��������������ƺ��Ҫ��AM=AN=CP=CQ����֪BC=24�ף�AB=40�ף���AN=x�ף��ֻ������Ϊy1ƽ���ף���ƺ���y2ƽ���ף�
��1���ֱ���y1��y2��x֮��ĺ�����ϵʽ����Ҫ��д���Ա�����ȡֵ��Χ����
��2����AN�ij�Ϊ������ʱ���ֻ������Ϊ440ƽ���ף�
��3�����ֻ�ÿƽ������200Ԫ�������ƺÿƽ������100Ԫ�������Ҫ���ֻ������������440ƽ���ף���ѧУ�������W��Ԫ������W��x֮��ĺ�����ϵʽ�������ѧУ������õ����ֵ��
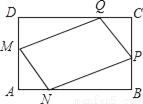
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡƽ���������2017-2018ѧ��ȵ�һѧ����ĩ��ѧ�Ծ����� ���ͣ���ѡ��
��ͼ����1=15�㣬��AOC=90�㣬��B��O��D��ͬһֱ���ϣ����2�Ķ���Ϊ��������

A. 75�� B. 105�� C. 15�� D. 165��
B ���������������� �ߡ�1=15�㣬��AOC=90�㣬���BOC=90��-15��=75�㣬���2=180��-��BOC=180��-75��=105�㣮��ѡB���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com