
定义新运算:a⊕b= 例如:4⊕5=
例如:4⊕5=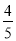 ,4⊕(﹣5)=
,4⊕(﹣5)=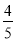 .则函数y=2⊕x(x≠0)的图象大致是( )
.则函数y=2⊕x(x≠0)的图象大致是( )
A. 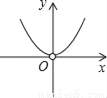 B.
B. 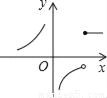 C.
C. 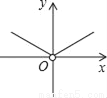 D.
D. 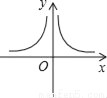
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源:重庆市秀山县2018届九年级上学期八校联考数学试卷 题型:单选题
二次函数y=ax2+bx+1(a≠0)的图象经过点(-1,0),则代数式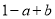 的值为( )
的值为( )
A. -3 B. -1 C. 2 D. 5
C 【解析】把(-1,0)代入y=ax2+bx+1得 a-b+1=0, ∴a-b=-1, ∴1-a+b=1-(a-b)=1-(-1)=2. 故选C.查看答案和解析>>
科目:初中数学 来源:四川省自贡市2016-2017学年上学期八年级期末统一考试数学试卷 题型:解答题
先化简,再求值: 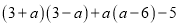 ,其中
,其中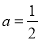
查看答案和解析>>
科目:初中数学 来源:2016-2017学年内蒙古呼和浩特市九年级(下)期中数学试卷 题型:解答题
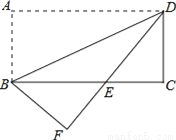
如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年内蒙古呼和浩特市九年级(下)期中数学试卷 题型:填空题
因式分解a3﹣4a的结果是 .
a(a+2)(a﹣2). 【解析】试题分析:原式提取a后,利用平方差公式分解即可. 【解析】 原式=a(a2﹣4) =a(a+2)(a﹣2). 故答案为:a(a+2)(a﹣2).查看答案和解析>>
科目:初中数学 来源:2016-2017学年内蒙古呼和浩特市九年级(下)期中数学试卷 题型:单选题
九年级一班和二班每班选8名同学进行投篮比赛,每名同学投篮10次,对每名同学投中的次数进行统计,甲说:“一班同学投中次数为6个的最多”乙说:“二班同学投中次数最多与最少的相差6个.”上面两名同学的议论能反映出的统计量是( )
A. 平均数和众数 B. 众数和极差 C. 众数和方差 D. 中位数和极差
B 【解析】试题分析:根据众数和极差的概念可知:一班同学投中次数为6个的最多反映出的统计量是众数,二班同学投中次数最多与最少的相差6个能反映出的统计量极差,故选B.查看答案和解析>>
科目:初中数学 来源:浙江省宁波市东钱湖九校2017-2018学年八年级上册数学期中联考试卷 题型:解答题
如图,在直角坐标系中,A、B、C、D各点的坐标分别为(﹣7,7)、(﹣7,1)、(﹣3,1)、(﹣1,4).
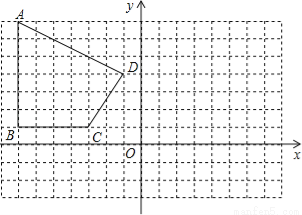
(1)在给出的图形中,画出四边形ABCD关于y轴对称的四边形A1B1C1D1; (不写作法)
(2)写出点A1和C1的坐标;
(3)求四边形A1B1C1D1的面积.
【解析】试题分析:(1)根据关于轴对称的点的坐标特点画出四边形即可; (2)根据各点在坐标系中的位置写出点和的坐标; (3)利用正方形的面积减去两角上三角形的面积即可. 试题解析:(1) (2)由(1)可得 (3)四边形查看答案和解析>>
科目:初中数学 来源:浙江省宁波市东钱湖九校2017-2018学年八年级上册数学期中联考试卷 题型:单选题
对于命题“如果∠1+∠2=90°,那么∠1≠∠2”,能说明它是假命题的反例是( )
A. ∠1=50°,∠2=40° B. ∠1=50°,∠2=50°
C. ∠1=∠2=45° D. ∠1=40°,∠2=40°
C 【解析】试题解析:由题干可知,当时, ,且满足∠1=∠2,故原命题是假命题. 故选C.查看答案和解析>>
科目:初中数学 来源:江苏省2018届九年级上学期期末模拟数学试卷 题型:解答题
(1)计算: 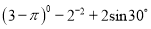 ; (2) 解方程:x2+4x+3=0.
; (2) 解方程:x2+4x+3=0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com