
(1)计算: 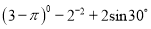 ; (2) 解方程:x2+4x+3=0.
; (2) 解方程:x2+4x+3=0.
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源:2016-2017学年内蒙古呼和浩特市九年级(下)期中数学试卷 题型:单选题
定义新运算:a⊕b= 例如:4⊕5=
例如:4⊕5=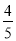 ,4⊕(﹣5)=
,4⊕(﹣5)=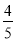 .则函数y=2⊕x(x≠0)的图象大致是( )
.则函数y=2⊕x(x≠0)的图象大致是( )
A. 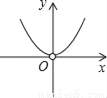 B.
B. 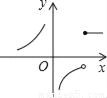 C.
C. 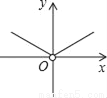 D.
D. 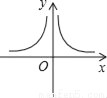
查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏苏州姑苏区第十中学初二上期中试卷数学试卷 题型:解答题
已知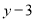 与
与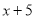 成正比例,且当
成正比例,且当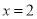 时,
时, 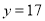 .求:
.求:
(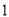 )
)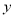 与
与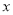 的函数关系.
的函数关系.
(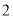 )当
)当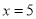 时,
时, 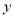 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏苏州姑苏区第十中学初二上期中试卷数学试卷 题型:单选题
函数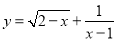 中自变量x的取值范围是( )
中自变量x的取值范围是( )
A. 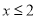 B.
B. 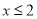 且
且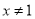 C. x<2且
C. x<2且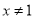 D.
D. 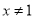
查看答案和解析>>
科目:初中数学 来源:江苏省2018届九年级上学期期末模拟数学试卷 题型:解答题
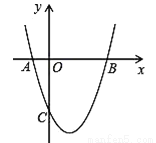
如图,抛物线y=x2 +bx+c与x轴交于A(﹣1,0),B(3,0)两点.
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
查看答案和解析>>
科目:初中数学 来源:江苏省2018届九年级上学期期末模拟数学试卷 题型:填空题
在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比.已知这本书的长为20 cm,则它的宽约为 .
12.36cm 【解析】设这本书的宽为xcm,由题意可得: , ∴. 故答案为:12.36cm.查看答案和解析>>
科目:初中数学 来源:江苏省2018届九年级上学期期末模拟数学试卷 题型:单选题
已知点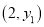 ,
, 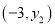 均在抛物线
均在抛物线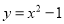 上,则
上,则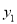 、
、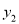 的大小关系为( )
的大小关系为( )
A. 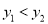 B.
B. 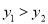 C.
C. 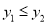 D.
D. 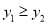
查看答案和解析>>
科目:初中数学 来源:山东省临朐县沂山风景区2017-2018学年七年级上期末模拟数学试卷 题型:填空题
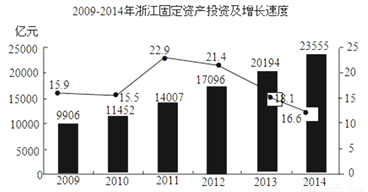
根据2009﹣2014年浙江固定资产投资(单位:亿元)及增速统计图所提供的信息,下列判断正确的是________
①2011年增长最快;
②2011、2012两年的年平均增长率为22.15%;
③从2011年开始增速逐年减少;
④各年固定资产投资的中位数是15586.5.
查看答案和解析>>
科目:初中数学 来源:2017年湖北省中考数学模拟试卷 题型:解答题
某文具店销售甲、乙两种圆规,当销售5只甲种、1只乙种圆规,可获利润25元,销售6只甲种、3只乙种圆规,可获利润39元.
(1)问该文具店销售甲、乙两种圆规,每只的利润分别是多少元?
(2)在(1)中,文具店共销售甲、乙两种圆规50只,其中甲种圆规为a只,求文具店所获得利润P与a的函数关系式,并求当a≥30时P的最大值.
(1)甲种圆规每只的利润是4元,乙种圆规每只的利润是5元;(2)220. 【解析】试题分析:(1)设文具店销售甲、乙两种圆规,每只的利润分别是x元、y元,根据题意“销售5只甲种、1只乙种圆规,可获利润25元,销售6只甲种、3只乙种圆规,可获利润39元”,列出的方程组,解方程组即可;(2)根据题意可以列出文具店所获利p与a的函数关系式,然后根据当a≥30,可以求得p的最大值即可. 试题解...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com