练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知有理数a、b、c在数轴上的对应点如图所示，|a-b|+|b-c|-|c-a|的结果（ ）

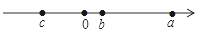
    A. a-b B. b+c C. 0 D. a-c

    C 【解析】【解析】 由数轴上点的位置得：c＜0＜b＜a，|a|＞|c|，∴a-b＞0，b-c＞0，c-a＜0，则|a-b|+|b-c|-|c-a|=a-b+b-c+c-a=0．故选C．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版初中数学七年级下册第八章《二元一次方程组》同步练习 题型：填空题

    若x－y＝7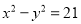， ，则3x+5y＝__________。

    5 【解析】∵x－y＝7， ， ∴x+y=3； 解方程组可得 ， ∴3x+5y＝3×5+5×（-2）=5.

    查看答案和解析>>

    科目：初中数学 来源：2018届中考数学一轮复习单元检测：第6讲 分式方程及其应用 题型：单选题

    解分式方程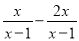＝1，可知方程的解为(　　)

    A. x＝1 B. x＝3 C. x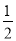＝ D. 无解

    C 【解析】方程两边同时乘以（x-1），得：x-2x=x-1， 解得：x＝， 检验：当x＝时，x-1≠0，所以x＝是分式方程的解， 故选C.

    查看答案和解析>>

    科目：初中数学 来源：广西北海市银海区2017年秋季学期教学质量监测七年级数学试卷 题型：解答题

    综合题：先化简，再求值

    （1）先化简，再求值：x 2 -（x+2）（2-x）-2（x-5） 2 ， 其中x=3．

    （2）解不等式组 ，并求它的整数解．

    （1） 6 （2） 1，2，3 【解析】试题分析：（1）先对x2﹣（x+2）（2﹣x）﹣2（x﹣5）2化简，再代入x的值. (2)先求每个不等式的解集，再求公共解，再写出其中的整数解即可. 试题解析： （1）x2–(4–x2)–2(x2–10x+25) =x2–4+x2–2x2+20x–50 =20x-54 . 把x=3代入上式，得 原式= 20×3...

    查看答案和解析>>

    科目：初中数学 来源：广西北海市银海区2017年秋季学期教学质量监测七年级数学试卷 题型：单选题

    将如图所示的两个平面图形绕轴旋转一周，对其所得的立体图形，下列说法正确的是（ ）

    主视图相同 B．左视图相同 C．俯视图相同 D．三种视图都不相同

    D 【解析】第一个得到的图形是圆锥，第二个得到的图形是圆柱，圆锥的主视图、左视图都是三角形，俯视图是圆和圆锥的顶点，圆柱的主视图、左视图是矩形，俯视图是圆，故三种视图都不相同，故选D

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级下册数学 第26章 反比例函数 单元检测卷 题型：解答题

    如图，一次函数y=﹣x+4的图象与反比例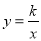（k为常数，且k≠0）的图象交于A（1，a），B两点．

    （1）求反比例函数的表达式及点B的坐标；

    （2）在x轴上找一点P，使PA+PB的值最小，求PA+PB的最小值．

    (1) 反比例函数的表达式y=，点B坐标（3，1）(2) . 【解析】试题分析：（1）把点A（1，a）代入一次函数y=-x+4，即可得出a，再把点A坐标代入反比例函数y=，即可得出k，两个函数解析式联立求得点B坐标； （2）作点B作关于x轴的对称点D，连接AD，交x轴于点P，此时PA+PB=PA+PD=AD的值最小，然后根据勾股定理即可求得． 试题解析：（1）把点A（1，a）代入...

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级下册数学 第26章 反比例函数 单元检测卷 题型：填空题

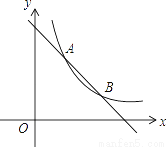
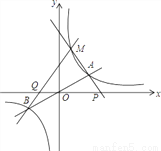
    如图，已知双曲线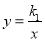与直线y=k2x（k1，k2都为常数）相交于A，B两点，在第一象限内双曲线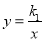上有一点M（M在A的左侧），设直线MA，MB分别与x轴交于P，Q两点，若MA=m•AP，MB=n•QB，则n﹣m的值是________．

    2 【解析】【解析】 作MH⊥y轴，AN⊥y轴，BI⊥y轴分别于点H、N、I，则MH∥AN∥BI． ∵反比例函数是中心对称图形，∴ON=OI． ∵MH∥AN∥BI，MA=m•AP，MB=n•QB， ∴m=，n=．又∵ON=OI，∴n= +2=m+2，∴n﹣m=2．故答案为：2．

    查看答案和解析>>

    科目：初中数学 来源：河南省新乡市卫辉市2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

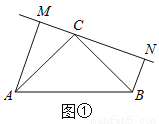
    如图①：在△ABC中，∠ACB=90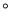，△ABC是等腰直角三角形，过点C在△ABC外作直线MN，AM⊥MN于点M，BN⊥MN于点N.

    （1）求证：MN=AM+BN.

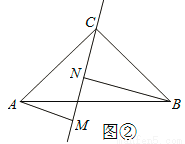
    （2）如图②，若过点C在△ABC内作直线MN，AM⊥MN于点M，BN⊥MN于点N，则猜想AM、BN与MN之间有什么关系？请直接写出结论，并写出图②中的全等三角形.

    （1）见解析；(2)MN=BN-AM (或AM=BN-MN或BN=AM+MN) 【解析】试题分析： （1）由AM⊥MN于点M，BN⊥MN于点N可得∠AMC=∠BNC=∠ACB=90°，由此可得∠MAC+∠ACM=90°，∠ACM+∠BCN=90°，从而可得∠MAC=∠BCN，结合AC=BC，即可证得△ACM≌△CBN，即可得到MC=BN，AM=CN，结合MN=MC+CN可得MN=AM+...

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级下册数学 第27章 相似 单元检测卷 题型：单选题

    若△ABC∽△A′B′C′，∠A=40°，∠C=110°，则∠B′等于（ ）

    A. 30° B. 50° C. 40° D. 70°

    A 【解析】试题分析：根据三角形内角和定理可得：∠B=30°，根据相似三角形的性质可得：∠B′=∠B=30°.

    查看答案和解析>>

    同步练习册答案