
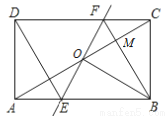
如图,矩形ABCD中,O为AC的中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④MB∶OE=3∶2.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
C 【解析】连接BD, ∵四边形ABCD是矩形, ∴AC=BD,AC、BD互相平分, ∵O为AC中点, ∴BD也过O点, ∴OB=OC, ∵∠COB=60°,OB=OC, ∴△OBC是等边三角形, ∴OB=BC=OC,∠OBC=60°, 在△OBF与△CBF中, , ∴△OBF≌△CBF(SSS), ∴△OBF与△CBF关于直... 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源:2017年广东省韶关市南雄市中考数学模拟试卷 题型:单选题
在一个不透明的口袋中,装有5个红球3个白球,它们除颜色外都相同,从中任意摸出一个球,摸到红球的概率为( )
A. 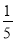 B.
B. 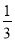 C.
C. 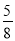 D.
D. 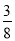
查看答案和解析>>
科目:初中数学 来源:山东省德州市2017-2018学年九年级上学期期中考试数学试卷 题型:填空题
已知点(m,n)在抛物线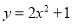 的图象上,则
的图象上,则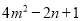 =__________.
=__________.
查看答案和解析>>
科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期末测试 题型:解答题
某剧院举行专场音乐会,成人票每张20元,学生票每张5元,暑假期间,为了丰富广大师生的业余文化生活,影剧院制定了两种优惠方案,方案1:购买一张成人票赠送一张学生票;
方案2:按总价的90%付款.
某校有4名老师与若干名(不少于4人)学生听音乐会.
(1)设学生人数为x(人),付款总金额为y(元),分别建立两种优惠方案中y与x的函数解析式;
(2)请计算并确定出最节省费用的购票方案.
(1)按优惠方案1得y1=5x+60(x≥4),按优惠方案2得y2=4.5x+72(x≥4); (2)当x=24时,两种优惠方案付款一样多;4≤x<24时,y1<y2,优惠方案1付款较少;x>24时,y1>y2,优惠方案2付款较少. 【解析】试题分析:(1)首先根据优惠方案①:付款总金额=购买成人票金额+除去4人后的学生票金额;优惠方案②:付款总金额=(购买成人票金额+购买学生票金额)...查看答案和解析>>
科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期末测试 题型:填空题
如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上.若∠1=20°,则∠2=____________.
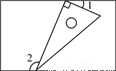
查看答案和解析>>
科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期末测试 题型:单选题
如图,将?ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B为( )
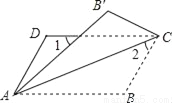
A. 66° B. 104° C. 114° D. 124°
C 【解析】试题解析:∵四边形ABCD是平行四边形, ∴AB∥CD, ∴∠ACD=∠BAC, 由折叠的性质得:∠BAC=∠B′AC, ∴∠BAC=∠ACD=∠B′AC= ∴∠B=180°-∠2-∠BAC=180°-44°-22°=114°; 故选C.查看答案和解析>>
科目:初中数学 来源:江西省2017-2018学年度八年级第三次月考数学试卷 题型:解答题
如图1,在平面直角坐标系xOy中,直线MN分别与x轴正半轴、y轴正半轴交于点M、N,且OM=6cm,∠OMN=30°,等边△ABC的顶点B与原点O重合,BC边落在x轴的正半轴上,点A恰好落在线段MN上,如图2,将等边△ABC从图1的位置沿x轴正方向以1cm/s的速度平移,边AB、AC分别与线段MN交于点E、F,在△ABC平移的同时,点P从△ABC的顶点B出发,以2cm/s的速度沿折线B→A→C运动,当点P达到点C时,点P停止运动,△ABC也随之停止平移.设△ABC平移时间为t(s),△PEF的面积为S(cm2).
(1)求等边△ABC的边长;
(2)当点P在线段BA上运动时,求S与t的函数关系式,并写出自变量t的取值范围;
(3)点P沿折线B→A→C运动的过程中,是否在某一时刻,使△PEF为等腰三角形?若存在,求出此时t值;若不存在,请说明理由.
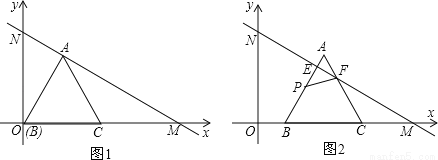
查看答案和解析>>
科目:初中数学 来源:江西省2017-2018学年度八年级第三次月考数学试卷 题型:单选题
如图所示,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC.∠EBC=∠E=60°,若BE=6,DE=2,则BC的长度是( )
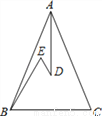
A.6 B.8 C.9 D.10
B 【解析】延长ED交BC于M,延长AD交BC于N,作DF∥BC, ∵AB=AC,AD平分∠BAC, ∴AN⊥BC,BN=CN, ∵∠EBC=∠E=60°, ∴△BEM为等边三角形, ∴△EFD为等边三角形, ∵BE=6,DE=2, ∴DM=4, ∵△BEM为等边三角形, ∴∠EMB=60°, ∵AN⊥BC, ∴∠DNM=90...查看答案和解析>>
科目:初中数学 来源:山西省2017-2018学年八年级上期末模拟数学试卷 题型:填空题
在实数范围内因式分【解析】
x3﹣2x2y+xy2=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com