练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知点（m，n）在抛物线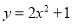的图象上，则=__________．

    -1 【解析】将(m,n)代入y=2x2+1得,n=2m2+1， 整理得：2m2?n=?1， ∴4m2?2n+1=2(2m2?n)+1=2×(?1)+1=?1 故答案为：?1.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

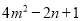    科目：初中数学 来源：河南省2017-2018学年七年级（上）期中数学试卷（解析版） 题型：单选题

    已知点O是线段AB上的一点，且AB=12cm，点M、N分别是线段AO、线段BO的中点，那么线段MN的长度是（　　）

    A. 6cm B. 5cm C. 4cm D. 无法确定

    A 【解析】∵点O是线段AB上一点， ∴AO+BO=AB=12． ∵点M、N分别是线段AO、线段BO的中点， ∴MO=AO，NO=BO． ∴MN=MO+NO=（AO+BO）=6（cm）. 故选：A．

    查看答案和解析>>

    科目：初中数学 来源：河南省2017-2018学年八年级上期末模拟数学试卷 题型：解答题

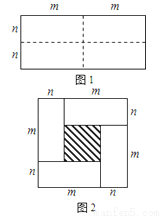
    图1是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图2的形状拼成一个正方形．

    （1）请写出图2中阴影部分的面积；

    （2）观察图2你能写出下列三个代数式之间的等量关系吗？

    代数式：（m+n）2， （m﹣n）2， mn；

    （3）根据（2）中的等量关系，解决如下问题：若a+b=7，ab=5，求（a﹣b）2的值．

    （1）（m﹣n）2或（m+n）2﹣4mn；（2）（m﹣n）2=（m+n）2﹣4mn；（3）29 【解析】试题分析：（1）方法一：求出正方形的边长，再根据正方形面积公式求出即可；方法二：根据大正方形面积减去4个矩形面积，即可得出答案；（2）根据两种表示阴影部分的面积的方法，即可得出等式；（3）根据等式（a-b）2=（a+b）2-4ab即可解决． 试题解析： （1）（m﹣n）2或（m...

    查看答案和解析>>

    科目：初中数学 来源：河南省2017-2018学年八年级上期末模拟数学试卷 题型：单选题

    下列四边形中，对角线相等且互相垂直平分的是（   ）

    A. 平行四边形 B. 正方形 C. 等腰梯形 D. 矩形

    B 【解析】试题解析：对角线相等且互相垂直平分的四边形是正方形， 故选B．

    查看答案和解析>>

    科目：初中数学 来源：山东省德州市2017-2018学年九年级上学期期中考试数学试卷 题型：解答题

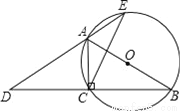
    如图，AB为⊙O的直径，点C在⊙O上，延长BC至点D，使DC=CB，延长DA与⊙O的另一个交点为E，连接AC，CE．

    （1）求证：∠B=∠D；

    （2）若AB=4，BC﹣AC=2，求CE的长．

    （1）证明见解析；（2）CE=1+. 【解析】试题分析：（1）由AB为⊙O的直径，易证得AC⊥BD，又由DC=CB，根据线段垂直平分线的性质，可证得AD=AB，即可得：∠B=∠D； （2）首先设BC=x，则AC=x-2，由在Rt△ABC中，AC2+BC2=AB2，可得方程：（x-2）2+x2=42，解此方程即可求得CB的长，继而求得CE的长． 试题解析：（1）证明：∵AB为⊙O的...

    查看答案和解析>>

    科目：初中数学 来源：山东省德州市2017-2018学年九年级上学期期中考试数学试卷 题型：单选题

    一小球被抛出后，距离地面的高度h(米)和飞行时间t(秒)满足下面函数关系式：h＝－5(t－1)2＋6，则小球距离地面的最大高度是(　 　)

    A. 1米 B. 5米 C. 6米 D. 7米

    C 【解析】试题解析：∵高度h和飞行时间t 满足函数关系式：h=-5（t-1）2+6， ∴当t=1时，小球距离地面高度最大， ∴h=-5×（1-1）2+6=6米， 故选C．

    查看答案和解析>>

    科目：初中数学 来源：山东省德州市2017-2018学年九年级上学期期中考试数学试卷 题型：单选题

    已知函数y＝kx＋b的图象如图，则一元二次方程x2＋x＋k－1＝0根的存在情况是(　　)

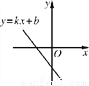
    A. 没有实数根; B. 有两个相等的实数根

    C. 有两个不相等的实数根; D. 无法确定

    C 【解析】试题分析：先根据函数y=kx+b的图象可得，k＜0，b＜0，再根据一元二次方程+x+k﹣1=0中，△=﹣4×1×（k﹣1）=5﹣4k＞0，则一元二次方程+x+k﹣1=0根的存在情况是有两个不相等的实数根. 故选：C．

    查看答案和解析>>

    科目：初中数学 来源：2018年春人教版八年级数学下册（广西）期末测试 题型：单选题

    如图，矩形ABCD中，O为AC的中点，过点O的直线分别与AB，CD交于点E，F，连接BF交AC于点M，连接DE，BO.若∠COB＝60°，FO＝FC，则下列结论：①FB⊥OC，OM＝CM；②△EOB≌△CMB；③四边形EBFD是菱形；④MB∶OE＝3∶2.其中正确结论的个数是（ ）

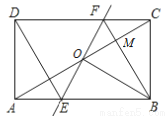
    A. 1 B. 2 C. 3 D. 4

    C 【解析】连接BD， ∵四边形ABCD是矩形， ∴AC=BD，AC、BD互相平分， ∵O为AC中点， ∴BD也过O点， ∴OB=OC， ∵∠COB=60°，OB=OC， ∴△OBC是等边三角形， ∴OB=BC=OC，∠OBC=60°， 在△OBF与△CBF中， ， ∴△OBF≌△CBF（SSS）， ∴△OBF与△CBF关于直...

    查看答案和解析>>

    科目：初中数学 来源：2017年广西南宁八中中考数学五模试卷 题型：解答题

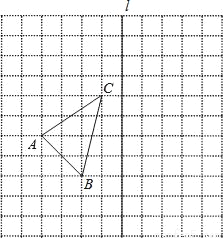
    如图，在11×11的正方形网格中，每个小正方形的边长都为1，网格中有一个格点△ABC（即三角形的顶点都在格点上）．

    （1）在图中作出△ABC关于直线l对称的△A1B1C1；（要求A与A1，B与B1，C与C1相对应）

    （2）作出△ABC绕点C顺时针方向旋转90°后得到的△A2B2C；

    （3）在（2）的条件下直接写出点B旋转到B2所经过的路径的长．（结果保留π）

    (1)作图见解析；（2）作图见解析；（3）. 【解析】【解析】 （1）△A1B1C1如图所示； （2）△A2B2C如图所示； （3）根据勾股定理，BC==， ∴点B旋转到B2所经过的路径的长==π.

    查看答案和解析>>

    同步练习册答案