
解不等式: 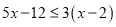 ,并把解在数轴上表示出来。
,并把解在数轴上表示出来。

 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源:江苏省2017-2018学年七年级12月月考数学试卷 题型:填空题
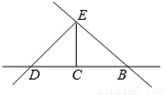
如图所示,图中共有线段__条.
查看答案和解析>>
科目:初中数学 来源:湖北省武汉市青山区2017-2018学年七年级(上)期中数学试卷 题型:解答题
如图1,点A,B,O,C为数轴上四点,点A对应数a(a<﹣2),点O对应0,点C对应3,AB=2 (AB表示点A到点B的距离).
(1)填空:点C到原点O的距离 ,:点B对应的数 .(用含有a的式子)
(2)如图2,将一刻度尺放在数轴上,刻度尺上“6cm”和“8.7cm”分别对应数轴上的点O和点C,若BC=5,求a的值和点A在刻度尺上对应的刻度.
(3)如图3,在(2)的条件下,点A以1单位长度/秒的逮度向右运动,同时点C向左运动,若运动3秒时,点A和点C到原点D的距离相等,求点C的运动速度.)
查看答案和解析>>
科目:初中数学 来源:湖北省武汉市青山区2017-2018学年七年级(上)期中数学试卷 题型:单选题
13世纪数学家斐波那契的《计算书》中有这样一个问题:“在罗马有7位老妇人,每人赶着7头毛驴,每头驴驮着7只口袋,每只口袋里装着7个面包,则面包数量为( )
A. 7×4 B. 7×7 C. 74 D. 76
C 【解析】试题解析:利用乘方的意义计算得:面包数量为74, 故选C查看答案和解析>>
科目:初中数学 来源:浙江省2017-2018学年八年级上学期第二次学情检测数学试卷 题型:解答题
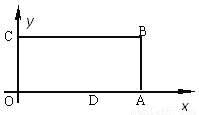
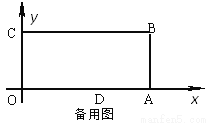
已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、C、D的坐标分别为A(9,0)、C(0,4),D(5,0),点P从点O出发,以每秒1个单位长度的速度沿O[Math Processing Error] 
 C[Math Processing Error]
C[Math Processing Error] 
 B[Math Processing Error]
B[Math Processing Error] 
 A运动,点P的运动时间为t秒.
A运动,点P的运动时间为t秒.
(1)当t=5时, P点坐标为____________;
(2)当t>4时,OP+PD有最小值吗?如果有,请算出该最小值,如果没有,请说明理由;
(3)当t为何值时,△ODP是腰长为5的等腰三角形?(直接写出t的值).
查看答案和解析>>
科目:初中数学 来源:浙江省2017-2018学年八年级上学期第二次学情检测数学试卷 题型:填空题
命题“同位角相等,两直线平行”的逆命题是: .
两直线平行,同位角相等. 【解析】试题分析:把一个命题的题设和结论互换就得到它的逆命题. 【解析】 命题:“同位角相等,两直线平行.”的题设是“同位角相等”,结论是“两直线平行”. 所以它的逆命题是“两直线平行,同位角相等.” 故答案为:“两直线平行,同位角相等”.查看答案和解析>>
科目:初中数学 来源:浙江省2017-2018学年八年级上学期第二次学情检测数学试卷 题型:单选题
在Rt△ABC中,∠ACB=90°,D是AB的中点,若AB=8,则CD的长为( )
A. 6 B. 5 C. 4 D. 3
C 【解析】∵在Rt△ABC中,∠ACB=90°,D是AB的中点, ∴CD=AB, 又∵AB=8, ∴CD=4. 故选C.查看答案和解析>>
科目:初中数学 来源:江苏省南通市2018届九年级上学期第三次月考数学试卷 题型:填空题
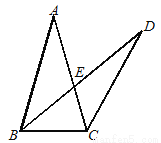
如图,在△ABC中,AB=AC=6,∠A=2∠BDC, BD交AC边于点E,且AE=4,则BE·DE=____________.
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市2017-2018学年七年级上学期中考试数学试卷 题型:单选题
下列计算正确的是( ).
A. 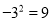 B.
B. 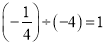 C.
C. 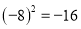 D.
D. 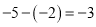
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com