
科目:初中数学 来源:湖北省孝感市八校联谊2017-2018学年九年级上册数学12月联考试卷 题型:单选题
抛物线y=2x2-12x+22 的顶点是( )
A. (3,-4) B. (-3,4) C. (3,4) D. (2,4)
C 【解析】∵, ∴抛物线的顶点坐标为(3,4). 故选C.查看答案和解析>>
科目:初中数学 来源:北京市海淀区2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
如图,在平面直角坐标系xOy中,△DEF可以看作是△ABC经过若干次的图形变化(轴对称、平移)得到的,写出一种由△ABC得到△DEF的过程:____________.

查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年七年级12月月考数学试卷 题型:解答题
某中学组织七年级学生参观,原计划租用45座客车若干辆,但有15人没有座位;如果租用同样数量的60座客车,则多出一辆,且其余客车恰好坐满.试问:
(1)七年级学生人数是多少?
(2)原计划租用45座客车多少辆?
(1)240;(2)5. 【解析】此题注意总人数是不变的,租用客车数也不变,设七年级人数是x人,客车数为,也可表示为+1,列方程即可解得. 【解析】 (1)设七年级人数是x人, 根据题意得=+1, 解得:x=240.故七年级学生人数是240人. (2)原计划租用45座客车:(240﹣15)÷45=5(辆). 故原计划租用45座客车5辆.查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年七年级12月月考数学试卷 题型:填空题
下图中,(1)请在横线上直接写出第1个和第2个几何体的名称,(2) 第3个和第4个图形是某些几何体的平面展开图,请判断后在横线上写出相应的几何体的名称.
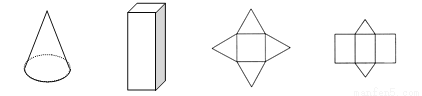

__________ __________ ___________ ____________
圆锥、长方体、四棱锥、三棱柱 【解析】由题意得, 圆锥、长方体、四棱锥、三棱柱.查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年七年级12月月考数学试卷 题型:单选题
在直线l上顺次取A、B、C三点,使得AB=5cm,BC=3cm,如果O是线段AC的中点,那么线段OB的长度是( )
A. 0.5cm B. 1cm C. 1.5cm D. 2cm
B 【解析】试题分析:作图分析 由已知条件可知,AB+BC=AC,又因为O是线段AC的中点,则OB=AB﹣AO,故OB可求. 【解析】 根据上图所示OB=5cm﹣OA, ∵OA=(AB+BC)÷2=4cm, ∴OB=1cm. 故选B.查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年七年级12月月考数学试卷 题型:单选题
如图,四个图形是由立体图形展开得到的,相应的立体图形顺次是( )
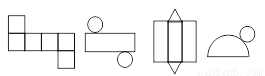
A. 正方体、圆柱、三 棱柱、圆锥
B. 正方体、圆锥、三棱柱、圆柱
C. 正方体、圆柱、三棱锥、圆锥
D. 正方体、圆柱 、四棱柱、圆锥
A 【解析】试题分析:根据正方体、圆柱、三棱柱、圆锥表面展开图的特点解题. 【解析】 观察图形,由立体图形及其表面展开图的特点可知相应的立体图形顺次是正方体、圆柱、三棱柱、圆锥. 故选C.查看答案和解析>>
科目:初中数学 来源:福建省2017-2018学年九年级数学上学期期末检测试卷 题型:单选题
如图,有一圆锥形粮堆,其侧面展开图是半径为6m的半圆,粮堆母线AC的中点P处有一老鼠正在偷吃粮食,此时,小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程长为( )
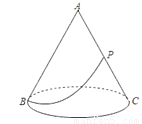
A. 3m B. 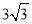 m C.
m C. 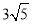 m D. 4m
m D. 4m
查看答案和解析>>
科目:初中数学 来源:浙江省2017-2018学年八年级上学期第二次学情检测数学试卷 题型:解答题
解不等式: 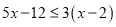 ,并把解在数轴上表示出来。
,并把解在数轴上表示出来。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com