
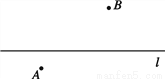
如图,已知直线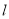 及其两侧两点A、B. (要求:保留作图痕迹,不需要证明)
及其两侧两点A、B. (要求:保留作图痕迹,不需要证明)
(1)在直线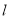 上求一点P,使PA=PB;
上求一点P,使PA=PB;
(2)在直线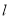 上求一点Q,使
上求一点Q,使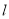 平分∠AQB.
平分∠AQB.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:浙江省宁波市东海实验学校2017年中考数学模拟试卷 题型:单选题
一名模型赛车手遥控一辆赛车,先前进1m,然后,原地逆时针方向旋转角a(0°<α<180°)。被称为一次操作.若五次操作后,发现赛车回到出发点,则角α为 ( )
A. 7 2° B. 108°或14 4° C. 144° D. 7 2°或144°
D 【解析】试题分析:因为赛车五次操作后回到出发点,五次操作一种是“正五边形“二种是“五角星“形,根据α最大值小于180°,经过五次操作,绝对不可能三圈或三圈以上.一圈360°或两圈720度.分别用360°和720°除以5,就可以得到答案. 【解析】 360÷5=72°, 720÷5=144°. 故选D.查看答案和解析>>
科目:初中数学 来源:2017年辽宁省中考数学二模试卷 题型:解答题
(本小题满分13分)
某公司经销农产品业务,以3万元/吨的价格向农户收购农产品后,以甲、乙两种方式进行销售,甲方式包装后直接销售;乙方式深加工后再销售.甲方式农产品的包装成本为1万元/吨,根据市场调查,它每吨平均销售价格y(单位:万元)与销售量m(单位:吨)之间的函数关系为y = -m+14(2≤m≤8);乙方式农产品深加工等(不含进价)总费用S(单位:万元)与销售量n(单位:吨)之间的函数关系是S=3n+12,平均销售价格为9万元/吨.
参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(-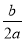 ,
,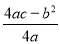 )
)
(1)该公司收购了20吨农产品,其中甲方式销售农产品x吨,其余农产品用乙方式销售,经销这20吨农产品所获得的毛利润为w万元(毛利润=销售总收入-经营总成本).
①直接写出:甲方式购买和包装x吨农产品所需资金为_________万元;乙方式购买和加工其余农产品所需资金为_________万元;
②求出w关于x的函数关系式;
③若农产品全部销售该公司共获得了48万元毛利润,求x的值;
④若农产品全部售出,该公司的最小利润是多少.
(2)该公司现有流动资金132万元,若将现有流动资金全部用于经销农产品,
①其中甲方式经销农产品x吨,则总经销量p为__________吨(用含x的代数式表示);
②当x为何值时,使公司获得最大毛利润,并求出最大毛利润.
(1)①4x,132-6x;②、w=;③、x=7;④、x=8,最小值为40;(2)①;②、以方式A销售4吨时,公司能获得最大毛利润64万元 【解析】 试题分析:(1)根据题意得出函数解析式;②、利用毛利润=销售总收入-经营总成本得出函数关系式;③、将w=48代入解析式求出x的值;④、根据函数的性质求出最值,(2)根据题意得出解析式;②、将m的值代入函数关系式,求出最值. 试题解析...查看答案和解析>>
科目:初中数学 来源:2017年辽宁省中考数学二模试卷 题型:单选题
一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4随机摸出一个小球,不放回,再随机摸出一个小球,两次摸出的小球标号的积小于4的概率是( )
A. 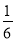 B.
B. 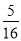 C.
C. 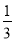 D.
D. 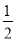
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市2017-2018学年八年级上学期教学水平监测数学试卷 题型:解答题
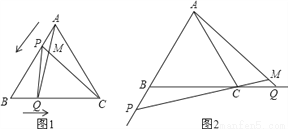
如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)△ABQ与△CAP全等吗?请说明理由;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在AB、BC的延长线上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,则求出它的度数.
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市2017-2018学年八年级上学期教学水平监测数学试卷 题型:填空题
在△ABC中,AB=15,AC=13,高AD=12,则BC的长是__________.
14或4 【解析】试题分析:本题应分两种情况进行讨论: (1)当△ABC为锐角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相加即为BC的长,从而可将△ABC的周长求出; (2)当△ABC为钝角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相减即为BC的长,从而可将△ABC的周长求出. 【解析】 此题...查看答案和解析>>
科目:初中数学 来源:四川省遂宁市2017-2018学年八年级上学期教学水平监测数学试卷 题型:单选题
如图在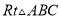 中,
中, 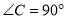 ,AD平分
,AD平分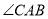 ,AC=6,BC=8,则CD的长为
,AC=6,BC=8,则CD的长为
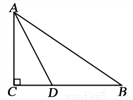
A. 1 B. 2 C. 3 D. 4
C 【解析】试题解析:过点D作DE⊥AB于E, ∵AD平分∠BAC, ∴CD=DE, 在Rt△ACD和Rt△AED中, , ∴Rt△ACD≌Rt△AED(HL), ∴AE=AC=6, 由勾股定理得,AB==10, ∴BE=AB-AE=10-6=4, 设CD=DE=x,则BD=8-x, 在Rt△BDE中,DE2+BE2=BD2, ...查看答案和解析>>
科目:初中数学 来源:2016-2017学年内蒙古呼伦贝尔市七年级(下)期中数学试卷 题型:解答题
如图,∠B=42°,∠1=∠2+10°,∠ACD=64°,∠ACD的平分线与BA的延长线相交于点E.
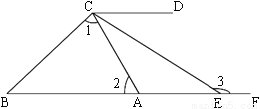
(1)请你判断BF与CD的位置关系,并说明理由;
(2)求∠3的度数.
(1)BF∥CD;(2)148° 【解析】 试题分析:(1)由∠B=42°,∠1=∠2+10°根据三角形的内角和定理可求得∠2=64°,再结合∠ACD=64°即可证得结论; (2)根据角平分线的性质可得∠DCE=∠ACD=32°,再根据平行线的性质求解即可. 【解析】 (1)BF∥CD,理由如下: 因为∠B=42°,∠1=∠2+10°,且三角形内角和为180° ...查看答案和解析>>
科目:初中数学 来源:2017-2018学年北师大版八年级数学下册 期中测评 题型:单选题
如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有( )
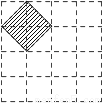
A. 2种B、3种C、4种D、5种
C 【解析】试题分析:利用轴对称图形的性质以及中心对称图形的性质分析得出符合题意的图形即可. 【解析】 如图所示:组成的图形是轴对称图形,又是中心对称图形, 则这个格点正方形的作法共有4种. 故选:C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com