
һ��ģ��������ң��һ����������ǰ��1m��Ȼ��ԭ����ʱ�뷽����ת��a(0��<��<180��)������Ϊһ�β���������β������������ص������㣬��Ǧ�Ϊ ( )
A. 7 2�� B. 108���14 4�� C. 144�� D. 7 2���144��
D �������������������Ϊ������β�����ص������㣬��β���һ���ǡ�������Ρ������ǡ�����ǡ��Σ����ݦ����ֵС��180�㣬������β��������Բ�������Ȧ����Ȧ���ϣ�һȦ360�����Ȧ720�ȣ��ֱ���360���720�����5���Ϳ��Եõ��𰸣� �������� 360��5=72�㣬 720��5=144�㣮 ��ѡD�� ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017�갲��ʡ�п���ѧ��ģ�Ծ� ���ͣ���ѡ��
��ͼ��С����һ�ž���ֽͼ��1���������߶���һ�ε�ͼ��2�����½��Խ��������غ��۵���ͼ��3������ͼ��4�����ۺ��е����غ϶�������������õ�����ͼ�Σ�������ͼ�ηֱ��ǣ�������

A. ���ǵ������� B. ���ǵȱ�������
C. ����ֱ�������Σ�һ������������ D. ����ֱ�������Σ�һ����������
C ���������ϸ���ͼ�е�˳�����϶��ۣ��ԽǶ�����ۣ����ۺ��е����غ϶����������չ���ɵõ�����ֱ�������Σ�һ�����������Σ���ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
�������εı߳�Ϊ1�������������__________
���������������� �ߴ˶����Ϊ�������Σ����AOB=360���6=60�㣬��OA=OB�����OAB�ǵȱ������Σ���OA=AB=1cm����OG=OA•cos30��=1��=����S��OAB=��AB��OG=��1��=cm����S������=6S��OAB=6��=cm���ʴ�Ϊ�� ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ�����ж���ʵ��ѧУ2017���п���ѧģ���Ծ� ���ͣ������
С���С���ڲٳ�����Ϸ���������ڵ��ϻ��˰뾶�ֱ�2m��3m��ͬ��Բ����ͼ������������һ����������Ȧ����Сʯ�ӣ�������ӰС��ʤ������С��ʤ��δ����Ȧ�ڲ��㣬���������У�
��1������Ϊ��Ϸ��ƽ��Ϊʲô��
��2����Ϸ������С�����߱��룬�����������ܷ���Ƶ�ʹ��Ƹ��ʵķ�����������ijһ������ͼ�ε�����ء���������Ʒ����������һ���⣮��Ҫ������ͼ�Σ�˵����Ʋ��衢ԭ����д�����㹫ʽ��
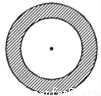
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ�����ж���ʵ��ѧУ2017���п���ѧģ���Ծ� ���ͣ������
��ͼ��ֱ��y=x��˫����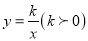 ��һ������ΪA����OA=2����k��ֵΪ�� ����
��һ������ΪA����OA=2����k��ֵΪ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ�����ж���ʵ��ѧУ2017���п���ѧģ���Ծ� ���ͣ���ѡ��
��ͼ��A��B�ǡ�O�ϵ����㣬AC�ǡ�O�����ߣ���OBA=75�㣬��O�İ뾶Ϊ1����OC�ij����ڣ�������
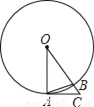
A. 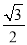 B.
B. 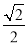 C.
C. 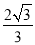 D.
D. 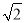
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�꽭��ʡ�������п���ѧһģ�Ծ� ���ͣ������
��ͼ�����κ���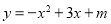 ��ͼ����x���һ������ΪB��4��0������һ������ΪA������y���ཻ��C�㣮
��ͼ����x���һ������ΪB��4��0������һ������ΪA������y���ཻ��C�㣮
��1����m��ֵ��C�����ꣻ
��2����ֱ��BC�Ϸ������������Ƿ����һ��M��ʹ������B��C���㹹�ɵ������������������ڣ������ʱM�����ꣻ�������ڣ����Ҫ˵�����ɣ�
��3��PΪ��������һ�㣬������ֱ��BC�ĶԳƵ�ΪQ��
�ٵ��ı���PBQCΪ����ʱ�����P�����ꣻ
�ڵ�P�ĺ�����Ϊt��0��t��4������tΪ��ֵʱ���ı���PBQC����������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�꽭��ʡ�������п���ѧһģ�Ծ� ���ͣ������
�ֽ���ʽ��xy2��2xy+x=_____��
x��y��1��2 ��������ԭʽ= . ����Ϊ�� .�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�ʡ������2017-2018ѧ����꼶��ѧ�ڽ�ѧˮƽ�����ѧ�Ծ� ���ͣ������
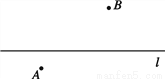
��ͼ����ֱ֪��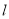 ������������A��B. ��Ҫ������ͼ�ۼ�������Ҫ֤����
������������A��B. ��Ҫ������ͼ�ۼ�������Ҫ֤����
��1����ֱ�� ����һ��P��ʹPA=PB��
����һ��P��ʹPA=PB��
��2����ֱ��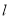 ����һ��Q��ʹ
����һ��Q��ʹ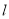 ƽ�֡�AQB��
ƽ�֡�AQB��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com