
���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�������н�������ȷ���ǣ�������
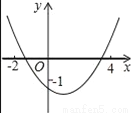
A. c����1 B. b��0 C. 2a+b��0 D. 9a+c��3b
D ������������������y��Ľ����ڵ㣨0����1�����·��õ�c����1���������߿��ڷ����a��0�����������ߵĶԳ�����y����Ҳ��a��b��ţ���b��0�����������ߵĶԳ��Եõ������߶Գ���Ϊֱ��x=������x=1����2a+b=0���ʿ��ܳ��������ڵ�x=��3ʱ��y��0������9a��3b+c��0����9a+c��3b�� �������� ����������y��Ľ����ڵ㣨0����1�����·��� ��c����1�� ... �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ������꼶��̰���ѧ�Ծ���C���� ���ͣ���ѡ��
��֪a��b��0����ô���в���ʽ��������ǣ� ��
A. 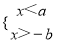 B.
B. 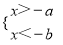 C.
C. 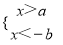 D.
D. 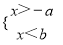
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭���ݹ�����������ѧ2017-2018ѧ�����꼶��ѧ���п�����ѧ�Ծ����������� ���ͣ������
�ҹ���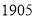 ���峯ѧ�õĿα����á�
���峯ѧ�õĿα����á�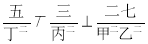 ������ʾ�൱�ڡ�
������ʾ�൱�ڡ�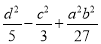 ������ô��
������ô��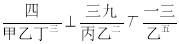 ����ʾ�൱��__________��
����ʾ�൱��__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017���Ĵ�ʡ�п���ѧģ���Ծ���3�� ���ͣ������
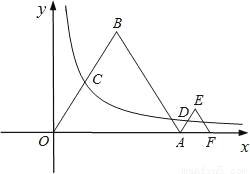
��ͼ���ȱߡ�OAB�͵ȱߡ�AFE��һ�߶���x���ϣ�˫����y=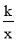 ��k��0��������OB���е�C��AE���е�D����֪�ȱߡ�OAB�ı߳�Ϊ4��
��k��0��������OB���е�C��AE���е�D����֪�ȱߡ�OAB�ı߳�Ϊ4��
��1�����˫��������ʾ�ĺ�������ʽ��
��2����ȱߡ�AEF�ı߳���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017���Ĵ�ʡ�п���ѧģ���Ծ���3�� ���ͣ������
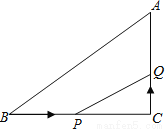
��ͼ���ڡ�ABC�У���C=90�㣬BC=16cm��AC=12cm����P�ӵ�B��������BC��2 cm /s���ٶ����C�ƶ�����Q�ӵ�C��������1cm/s���ٶ����A�ƶ�������P��Q�ֱ�ӵ�B��Cͬʱ���������˶�ʱ��Ϊts����t��________ʱ����CPQ���CBA���ƣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017���Ĵ�ʡ�п���ѧģ���Ծ���3�� ���ͣ���ѡ��
����x��һԪ���η���ax2��x+1=0��ʵ��������a��ȡֵ��Χ�ǣ� ��
A. a��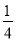 ��a��0 B. a��
��a��0 B. a��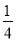 C. a��
C. a��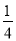 ��a��0 D. a��
��a��0 D. a��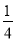
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ������꼶�˽̰���ѧ�Ծ���C���� ���ͣ������
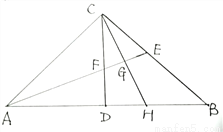
��ͼ���ڡ�ABC�У���ACB��90�㣬AC��BC����ABC�ĸ�CD���ƽ����AE�ཻ��F������C��CH��AE��G����AB��H��
��1�����BCH�Ķ�����
��2����֤��CE��BH��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ������꼶�˽̰���ѧ�Ծ���C���� ���ͣ���ѡ��
��ͼ���ڡ�ABC�У�AB=20cm��AC=12cm����P�ӵ�B������ÿ��3cm�ٶ����A�˶�����Q�ӵ�Aͬʱ������ÿ��2cm�ٶ����C�˶�������һ�����㵽��˵㣬��һ������Ҳ��ֹ֮ͣ������APQ����PQΪ�ĵ���������ʱ���˶���ʱ����( )��
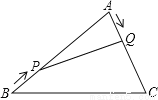
A. 2.5 B. 3 C. 3.5 D. 4
D ���������������� ���˶���ʱ��Ϊx���ڡ�ABC�У�AB=20cm��AC=12cm����P�ӵ�B������ÿ��3cm���ٶ����A�˶�����Q�ӵ�Aͬʱ������ÿ��2cm���ٶ����C�˶�������APQ�ǵ���������ʱ��AP=AQ��AP=20��3x��AQ=2x����20��3x=2x�����x=4����ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ������
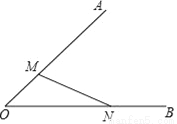
��ͼ������һ��P��ʹ��P����AOB���ߵľ�����ȣ�����ʹOP����MN����д������������ͼ�ۼ�����Ҫ���ó߹���ͼ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com