
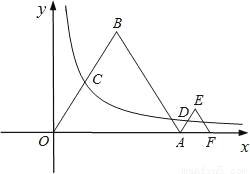
��ͼ���ȱߡ�OAB�͵ȱߡ�AFE��һ�߶���x���ϣ�˫����y=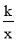 ��k��0��������OB���е�C��AE���е�D����֪�ȱߡ�OAB�ı߳�Ϊ4��
��k��0��������OB���е�C��AE���е�D����֪�ȱߡ�OAB�ı߳�Ϊ4��
��1�����˫��������ʾ�ĺ�������ʽ��
��2����ȱߡ�AEF�ı߳���
 ��У��������ĩ��̾�ϵ�д�
��У��������ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ������꼶��̰���ѧ�Ծ���C���� ���ͣ������
��ͼ����ƽ��ֱ������ϵxOy�У�����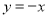 ��ͼ��
��ͼ��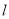 �ǵڶ��������Ľ�ƽ���ߣ�
�ǵڶ��������Ľ�ƽ���ߣ�

��1��ʵ����̽������ͼ�۲���֪A����1��3������ֱ��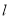 �ĶԳƵ�
�ĶԳƵ�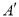 ������Ϊ����3��1��������д����B��5��3������ֱ��
������Ϊ����3��1��������д����B��5��3������ֱ��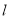 �ĶԳƵ�
�ĶԳƵ�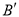 ������Ϊ ��
������Ϊ ��
��2�������뷢�֣����ͼ�Σ��Լ�ѡ������һ�ԣ�ͨ���۲������꣬��ᷢ�֣�����ƽ������һ��P��m ��n�����ڵڶ��������Ľ�ƽ����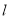 �ĶԳƵ�
�ĶԳƵ�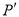 ������Ϊ ��
������Ϊ ��
��3���������ع㣺��֪����C��6 �� 0����D��2 �� 4��������ֱ��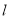 ��ȷ��һ�㣬ʹ��㵽C��D����ľ���֮����С����ͼ�л�������λ�ã�������ͼ�ۼ���������������꣮
��ȷ��һ�㣬ʹ��㵽C��D����ľ���֮����С����ͼ�л�������λ�ã�������ͼ�ۼ���������������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ������꼶��̰���ѧ�Ծ���A���� ���ͣ���ѡ��
��֪��P����2��1������ô��P����x��ԳƵĵ�P��������ǣ� ��
A��(��2��1) B��(��1��2) C��(2��1) D��(��2����1)
D �������� �������������x��ԳƵĵ�ĺ�������ͬ�������껥Ϊ�෴��. ��P����2��1������x��ԳƵĵ�P���������(��2����1)����ѡD.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭���ݹ�����������ѧ2017-2018ѧ�����꼶��ѧ���п�����ѧ�Ծ����������� ���ͣ������
��֪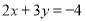 ����ô
����ô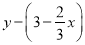 ��ֵ��__________��
��ֵ��__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭���ݹ�����������ѧ2017-2018ѧ�����꼶��ѧ���п�����ѧ�Ծ����������� ���ͣ���ѡ��
����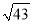 ��ֵ��ӽ��������ĸ������� ����
��ֵ��ӽ��������ĸ������� ����
A. 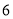 B.
B. 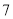 C.
C. 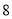 D.
D. 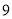
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017���Ĵ�ʡ�п���ѧģ���Ծ���3�� ���ͣ������
�ⷽ�̣���2x+1��2=2x+1��
x=0��x=. �����������������������ʽ�ֽⷨ��һԪ���η��̵Ľⷨ��ֱ�������������ab=0�Ĺ�ϵ��ⷽ�̼���. ����������ߣ�2x+1��2����2x+1��=0�� �ࣨ2x+1����2x+1��1��=0����2x��2x+1��=0�� ��x=0��2x+1=0�� ��ã�x=0��x=�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017���Ĵ�ʡ�п���ѧģ���Ծ���3�� ���ͣ���ѡ��
���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�������н�������ȷ���ǣ�������
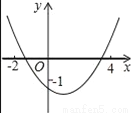
A. c����1 B. b��0 C. 2a+b��0 D. 9a+c��3b
D ������������������y��Ľ����ڵ㣨0����1�����·��õ�c����1���������߿��ڷ����a��0�����������ߵĶԳ�����y����Ҳ��a��b��ţ���b��0�����������ߵĶԳ��Եõ������߶Գ���Ϊֱ��x=������x=1����2a+b=0���ʿ��ܳ��������ڵ�x=��3ʱ��y��0������9a��3b+c��0����9a+c��3b�� �������� ����������y��Ľ����ڵ㣨0����1�����·��� ��c����1�� ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ������꼶�˽̰���ѧ�Ծ���C���� ���ͣ������
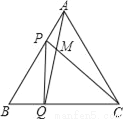
��ͼ����P��Q�ֱ��DZ߳�Ϊ4cm�ĵȱߡ�ABC��AB��BC�ϵĶ��㣬��P�Ӷ���A����Q�Ӷ���Bͬʱ�����������ǵ��ٶȶ�Ϊ1cm/s�������ĸ�������ȷ����________________��
��BP=CM���ڡ�ABQ�ա�CAP���ۡ�CMQ�Ķ������䣬ʼ�յ���60�㣻�ܵ���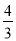 ����
���� ��ʱ����PBQΪֱ�������Σ�
��ʱ����PBQΪֱ�������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ С������ ���ͣ���ѡ��
��ͼ����ֱ������ϵ�У�ֱ��y1=2x��2�������ύ��A��B���㣬��˫����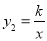 ��x��0�����ڵ�C������C��CD��x�ᣬ��OA=AD�������½��ۣ� �ٵ�x��0ʱ��y1��x�����������y2��x���������С��
��x��0�����ڵ�C������C��CD��x�ᣬ��OA=AD�������½��ۣ� �ٵ�x��0ʱ��y1��x�����������y2��x���������С��
��k=4��
�۵�0��x��2ʱ��y1��y2��
����ͼ����x=4ʱ��EF=4��
������ȷ���۵ĸ����ǣ� ��
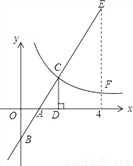
A. 1 B. 2 C. 3 D. 4
C ������������ֱ��y₁=2x?2�� ��x=0,�õ�y=2;��y=0,�õ�x=1, ��A(1,0),B(0,?2)����OA=1��OB=2�� �ڡ�OBA�͡�CDA��, �� ���OBA�ա�CDA(AAS)�� ��CD=OB=2��OA=AD=1�� ��C(2,2)�� ��x>0ʱ,y₁��x�����������,y₂��x���������С���ʢ���ȷ�� ��C������뷴������...�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com