
已知a>b>0,那么下列不等式组中无解的是( )
A. 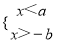 B.
B. 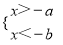 C.
C. 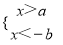 D.
D. 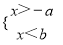
 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(七) 题型:单选题
如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点, 将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是 ( )
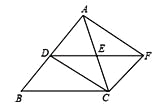
A. 矩形 B. 菱形 C. 正方形 D. 梯形
A 【解析】试题分析:根据旋转得到AD=CF,AD∥CF,则四边形ADCF为平行四边形,根据AC=BC,D为中点则∠ADC=90°,则四边形ADCF为矩形.查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年八年级12月月考数学试卷 题型:填空题
某校九年级甲、乙两班举行电脑汉字输入比赛,两个班能参加比赛的学生每分钟输入汉字的个数,经统计和计算后结果如下表:

有一位同学根据上面表格得出如下结论:
①甲、乙两班学生的平均水平相同;②乙班优秀人数比甲班优秀人数多(每分钟输入汉字达150个以上为优秀);③甲班学生比赛成绩的波动比乙班学生比赛成绩的波动大.
上述结论正确的是_______(填序号).
①②③. 【解析】根据平均数、方差和中位数的意义,可知:甲乙的平均数相同,所以①甲、乙两班学生的平均水平相同.根据中位数可知乙的中位数大,所以②乙班优秀的人数比甲班优秀的人数多.根据方差数据可知,方差越大波动越大,反之越小,所以甲班学生比赛成绩的波动比乙班学生比赛成绩的波动大. 故答案为:①②③.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级浙教版数学试卷(C卷) 题型:解答题
如图,在平面直角坐标系xOy中,函数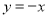 的图象
的图象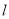 是第二、四象限的角平分线.
是第二、四象限的角平分线.

(1)实验与探究:由图观察易知A(-1,3)关于直线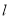 的对称点
的对称点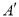 的坐标为(-3,1),请你写出点B(5,3)关于直线
的坐标为(-3,1),请你写出点B(5,3)关于直线 的对称点
的对称点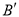 的坐标为 ;
的坐标为 ;
(2)归纳与发现:结合图形,自己选点再试一试,通过观察点的坐标,你会发现:坐标平面内任一点P(m ,n)关于第二、四象限的角平分线 的对称点
的对称点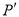 的坐标为 ;
的坐标为 ;
(3)运用与拓广:已知两点C(6 , 0),D(2 , 4),试在直线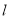 上确定一点,使这点到C,D两点的距离之和最小,在图中画出这点的位置,保留作图痕迹,并求出这点的坐标.
上确定一点,使这点到C,D两点的距离之和最小,在图中画出这点的位置,保留作图痕迹,并求出这点的坐标.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级浙教版数学试卷(C卷) 题型:填空题
如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为______.
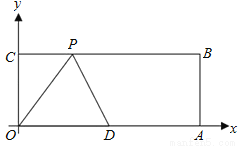
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级浙教版数学试卷(C卷) 题型:单选题
直线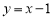 与两坐标轴分别交于A、B两点,点C在坐标轴上,若△ABC为等腰三角形,则满足条件的点C最多有( )
与两坐标轴分别交于A、B两点,点C在坐标轴上,若△ABC为等腰三角形,则满足条件的点C最多有( )
A.4个 B.5个 C.6个 D.7个
D. 【解析】 试题分析:直线与y轴的交点为A(0,﹣1),直线与x轴的交点为B(1,0). ①以AB为底,C在原点; ②以AB为腰,且A为顶点,C点有3种可能位置; ③以AB为腰,且B为顶点,C点有3种可能位置. 所以满足条件的点C最多有7个. 故选D.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级浙教版数学试卷(A卷) 题型:解答题
已知:如图,AB∥CD,E是AB的中点,CE=DE.求证:
(1)∠AEC=∠BED;
(2)AC=BD.
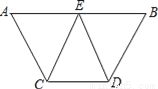
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级浙教版数学试卷(A卷) 题型:单选题
已知点P(-2,1),那么点P关于x轴对称的点P′的坐标是( )
A、(-2,1) B、(-1,2) C、(2,1) D、(-2,-1)
D 【解析】 试题分析:关于x轴对称的点的横坐标相同,纵坐标互为相反数. 点P(-2,1)关于x轴对称的点P′的坐标是(-2,-1),故选D.查看答案和解析>>
科目:初中数学 来源:2017年四川省中考数学模拟试卷(3) 题型:单选题
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
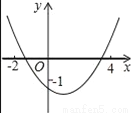
A. c>﹣1 B. b>0 C. 2a+b≠0 D. 9a+c>3b
D 【解析】由抛物线与y轴的交点在点(0,﹣1)的下方得到c<﹣1;由抛物线开口方向得a>0,再由抛物线的对称轴在y轴的右侧得a、b异号,即b<0;根据抛物线的对称性得到抛物线对称轴为直线x=﹣,若x=1,则2a+b=0,故可能成立;由于当x=﹣3时,y>0,所以9a﹣3b+c>0,即9a+c>3b. 【解析】 ∵抛物线与y轴的交点在点(0,﹣1)的下方. ∴c<﹣1; ...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com