练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    计算：tan30°cos60°+tan45°cos30°．

    . 【解析】试题分析：根据特殊角的三角函数值可以计算出tan30°cos60°+tan45°cos30°的值． 【解析】 tan30°cos60°+tan45°cos30° = = =．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年湖南省郴州市汝城县濠头学校中考数学模拟试卷 题型：解答题

    （1）解方程组： .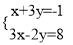

    （2）解不等式组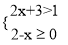并把解集在数轴上表示出来．

    （1），方程组的解为；（2）不等式组的解集为：﹣1＜x≤2，在数轴上表示见解析. 【解析】试题分析：（1）第一个方程两边乘以3变形后，减去第二个方程消去x求出y的值，进而求出x的值，即可确定出方程组的解； （2）分别求出不等式组中两不等式的解集，找出解集的公共部分即可确定出不等式组的解集，表示在数轴上即可． 试题解析：（1）， ①×3﹣②，得11y=﹣11， 解得：y...

    查看答案和解析>>

    科目：初中数学 来源：2017年天津市中考数学模拟试卷（1） 题型：单选题

    已知a，b，c在数轴上的位置如图所示，化简|a+c|-|a-2b|-|c+2b|的结果是（ ）

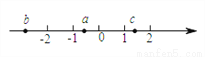
    A. 4b+2c B. 0 C. 2c D. 2a+2c

    A 【解析】由数轴上点的位置得：b|c|>|a|， ∴a+c>0，a?2b>0，c+2b<0， 则原式=a+c?a+2b+c+2b=4b +2c. 故选：B.

    查看答案和解析>>

    科目：初中数学 来源：2017年安徽省中考数学模拟试卷 题型：单选题

    为丰富学生课外活动，某校积极开展社团活动，学生可根据自己的爱好选择一项，已知该校开设的体育社团有：A：篮球，B：排球C：足球；D：羽毛球，E：乒乓球．李老师对某年级同学选择体育社团情况进行调查统计，制成了两幅不完整的统计图（如图），则以下结论不正确的是（　　）

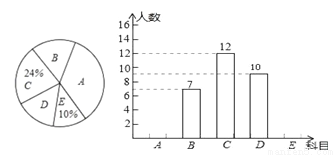
    A. 选科目E的有5人

    B. 选科目D的扇形圆心角是72°

    C. 选科目A的人数占体育社团人数的一半

    D. 选科目B的扇形圆心角比选科目D的扇形圆心角的度数少21.6°

    C 【解析】试题分析：A选项先求出调查的学生人数，再求选科目E的人数来判定， B选项利用×360°判定即可， C选项中求出B，C，D的人数即可判定， D选项利用选科目B的人数减选科目D，再除以总人数乘360°求解即可判定． 【解析】 调查的学生人数为：12÷24%=50（人），选科目E的人数为：50×10%=5（人），故A选项正确， 选科目D的扇形圆心角是×3...

    查看答案和解析>>

    科目：初中数学 来源：2017年广西防城港市中考数学模拟试卷 题型：解答题

    如图，某办公楼AB的后面有一建筑物CD，当光线与地面的夹角是22°时，办公楼在建筑物的墙上留下高2米的影子CE，而当光线与地面夹角是45°时，办公楼顶A在地面上的影子F与墙角C有25米的距离（B，F，C在一条直线上）．

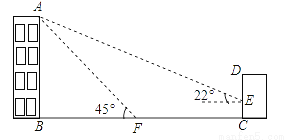
    （1）求办公楼AB的高度；

    （2）若要在A，E之间挂一些彩旗，请你求出A，E之间的距离．

    （参考数据：sin22°≈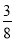，cos22°≈ 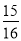，tan22°≈）

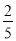    （1）教学楼的高20m；（2）A、E之间的距离约为48m． 【解析】（1）过点E作EM⊥AB于点M，设AB=x，在Rt△ABF中，由∠AFB=45°可知BF=AB=x， 在Rt△AEM中，利用锐角三角函数的定义求出x的值即可；（2）在Rt△AME中，根据cos22°=可得出结论． 【解析】 （1）过点E作EM⊥AB于点M，设AB=x， 在Rt△ABF中，∵∠AFB=45°...

    查看答案和解析>>

    科目：初中数学 来源：2017年广西防城港市中考数学模拟试卷 题型：填空题

    当x=___________时，二次根式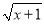取最小值，其最小值为___________。

    -1 0 【解析】根据二次根式有意义的条件，得x+1?0，则x??1. 所以当x=?1时，该二次根式有最小值，即为0. 故答案为：?1，0.

    查看答案和解析>>

    科目：初中数学 来源：2017年广西防城港市中考数学模拟试卷 题型：单选题

    计算2x3÷x2的结果是（　　）

    A. x B. 2x C. 2x5 D. 2x6

    B 【解析】试题分析：根据单项式除单项式的法则，同底数幂相除，底数不变指数相减的性质，对各选项计算后选取答案． 试题解析：2x3÷x2=2x． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：江苏省徐州市区联校2017-2018学年七年级上学期期中联考数学试卷 题型：填空题

    若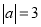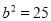， ，且a＜b，则2a－b的值为______.

    1或﹣11 【解析】试题解析：∵|a|=3，b2=25， ∴a=3或-3，b=5或-5， ∵a＜b， ∴a=3时，b=5，此时2a-b=2×3-5=1， a=-3时，b=5，此时2a-b=2×（-3）-5=-6-5=-11， 故答案为：1或-11．

    查看答案和解析>>

    科目：初中数学 来源：江苏省盐城市2017-2018学年八年级12月联合质量调研数学试卷 题型：解答题

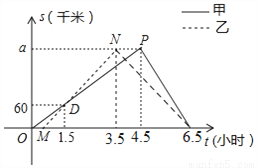
    顺丰快递公司派甲、乙两车从A地将一批物品匀速运往B地，甲出发0.5h后乙开始出发，结果比甲早1（h）到达B地，如图，线段OP、MN分别表示甲、乙两车离A地的距离S（km）与时间t（h）的关系，a表示A、B两地之间的距离．请结合图中的信息解决如下问题：

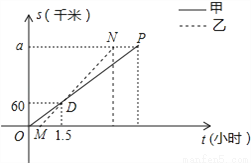
    （1）分别计算甲、乙两车的速度及a的值；

    （2）乙车到达B地后以原速立即返回，请问甲车到达B地后以多大的速度立即匀速返回，才能与乙车同时回到A地？并在图中画出甲、乙两车在返回过程中离A地的距离S（km）与时间t（h）的函数图象．

    【答案】（1）甲、乙两车的速度分别为40km/h、60km/h，a的值是180km；（2）甲返回时的速度为90km/h

    【解析】试题分析：（1）观察t轴，s轴表示的意义，利用v=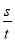求速度.(2) ，利用v=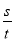为等量列方程求解.

    试题解析：

    （1）由图象得：甲的速度为：60÷1.5=40（km/h），

    乙的速度为：60÷（1.5﹣0.5）=60（km/h），

    求a的方法如下：

    方法1：由题意得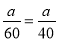： ﹣1﹣0.5，解得：a=180；

    方法2：设甲到达B地的时间为t时，则乙所用的时间为（t﹣1﹣0.5）时，

    由题意得：40t=60（t﹣1﹣0.5），

    t=4.5，

    ∴a=40t=40×4.5=180，

    答：甲、乙两车的速度分别为40km/h、60km/h，a的值是180km.

    （2）方法1：设甲返回时的速度为xkm/h，

    则,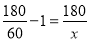

    解得：x=90，

    经检验：x=90是原方程的解，用符合题意，

    所以，甲返回时的速度为90km/h；

    方法2：甲、乙同时返回A地，则甲返回时所用的时间为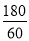： -1=2，

    所以，甲返回时的速度为：180÷2=90（km/h）．

    图象如图所示：

    【题型】解答题
    【结束】
    25

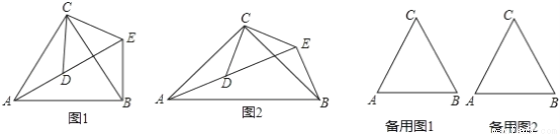
    （1）问题发现：如图1，△ACB和△DCE均为等边三角形，当△DCE旋转至点A，D，E在同一直线上，连接BE．

    填空：① ∠AEB的度数为_______；②线段AD、BE之间的数量关系是______．

    （2）拓展研究：

    如图2，△ACB和△DCE均为等腰三角形，且∠ACB=∠DCE=90°，点A、D、E在同一直线上，若AE=15，DE=7，求AB的长度．

    （3）探究发现：

    图1中的△ACB和△DCE，在△DCE旋转过程中当点A，D，E不在同一直线上时，设直线AD与BE相交于点O，试在备用图中探索∠AOE的度数，直接写出结果，不必说明理由．

    （1）60°．AD=BE；（2）AB=17；（3）∠AOE的度数是60°或120°． 【解析】试题分析：（1）由条件易证△ACD≌△BCE，从而得到：AD=BE，∠ADC=∠BEC．由点A，D，E在同一直线上可求出∠ADC，从而可以求出∠AEB的度数． （2）仿照（1）中的解法可求出∠AEB的度数，证出AD=BE；由△DCE为等腰直角三角形及CM为△DCE中DE边上的高可得CM=DM=...

    查看答案和解析>>

    同步练习册答案