
在一个不透明的盒子里,装有4个黑球和若干个白球,它们除颜色外没有任何其他区别.摇匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复,共摸球40次,其中10次摸到黑球,则估计盒子中大约有白球( )
A. 12个 B. 16个 C. 20个 D. 30个
A 【解析】试题分析:先算出盒子中黑球所占百分比,则,即共有20个球,则白球有个20÷100=20%,则4÷20%=20,即共有20个球,则白球有20-4=16个.故选B. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:初一数学第一学期4.3角同步练习 题型:单选题
一个人从A点出发向北偏东60°的方向走到B点,再从B出发向南偏西15°方向走到C点,那么∠ABC等于( )
A. 75° B. 105° C. 45° D. 135°
C 【解析】试题分析:首先根据方位角画出图形,从而可以得出∠ABC=60°-15°=45°,故选择C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期人教版八年级数学上11.2.1《三角形的内角和》同步练习题(含答案) 题型:解答题
如图,A点在B点的北偏东40°方向,C点在B点的北偏东75°方向,A点在C点的北偏西50°方向.求从A点观测B,C两点的视角∠BAC的度数.
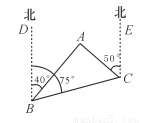
查看答案和解析>>
科目:初中数学 来源:2018年春九年级数学下册湘教版:单元测试(四) 概率 题型:解答题
某小区改善生态环境,实行生活垃圾的分类处理,将生活垃圾分成三类:厨房垃圾、可回收垃圾和其他垃圾,分别记为m,n,p,并且设置了相应的垃圾箱,“厨房垃圾”箱,“可回收垃圾”箱和“其他垃圾”箱,分别记为A,B,C.
(1)若将三类垃圾随机投入三类垃圾箱,请用画树状图的方法求垃圾投放正确的概率;
(2)为了了解居民生活垃圾分类投放的情况,现随机抽取了小区三类垃圾箱中总共1 000吨生活垃圾,数据统计如下(单位:吨):
A | B | C | |
m | 400 | 100 | 100 |
n | 30 | 240 | 30 |
p | 20 | 20 | 60 |
请根据以上信息,试估计“厨房垃圾”投放正确的概率.
(1)(2) 【解析】试题分析:(1)根据题意画出树状图,由树状图可知总数为9,投放正确有3种,进而求出垃圾投放正确的概率; (2)由题意和概率的定义易得所求概率. 试题解析:(1)画树状图如下: 共有9种等可能的结果数,其中垃圾投放正确的结果数为3,所以垃圾投放正确的概率为=. (2)=,所以估计“厨房垃圾”投放正确的概率为.查看答案和解析>>
科目:初中数学 来源:2018年春九年级数学下册湘教版:单元测试(四) 概率 题型:填空题
张凯家购置了一辆新车,爸爸妈妈商议确定车牌号,前三位选定为8ZK后,对后两位数字意见有分歧,最后决定由毫不知情的张凯从如图排列的四个数字中随机划去两个,剩下的两个数字从左到右组成两位数,续在8ZK之后,则选中的车牌号为8ZK86的概率是______.

查看答案和解析>>
科目:初中数学 来源:2018年春九年级数学下册湘教版:单元测试(四) 概率 题型:单选题
下列说法中正确的是( )
A. “打开电视机,正在播放《动物世界》”是必然事件
B. 某种彩票的中奖率为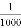 ,说明每买1 000张彩票,一定有一张中奖
,说明每买1 000张彩票,一定有一张中奖
C. 抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为
D. 想了解长沙市所有城镇居民的人均年收入水平,宜采用抽样调查
D 【解析】试题分析:根据随机事件,可判断A;根据概率的意义,可判断B、C;根据调查方式,可判断D. 【解析】 A、“打开电视机,正在播放《动物世界》”是随机事件,故A错误; B、某种彩票的中奖概率为,说明每买1000张,有可能中奖,也有可能不中奖,故B错误; C、抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为,故C错误; D、想了解长沙市所有城镇居民的人均年收入...查看答案和解析>>
科目:初中数学 来源:山西省大同市矿区2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
如图:△ABC的边BC的高为AF,AC边上的高为BG,中线为AD,AF=6,BC=12,BG=5.
(1)求△ABD的面积.
(2)求AC的长.
(3)△ABD和△ACD的面积有何关系.
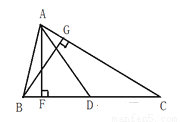
查看答案和解析>>
科目:初中数学 来源:2017年秋(北师大版)九年级数学下册(河南)检测:3.9 弧长及扇形的面积 题型:填空题
如图,在扇形AOB中,∠AOB=90°,以点A为圆心,OA的长为半径作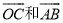 于点C,若OA=2,则阴影部分的面积为_____.
于点C,若OA=2,则阴影部分的面积为_____.
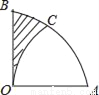
查看答案和解析>>
科目:初中数学 来源:湖南省醴陵市青云学校2016-2017学年七年级上学期期中考试数学试卷 题型:填空题
当 为________时,
为________时, 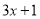 与
与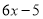 的值相等.
的值相等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com