
已知:如图,Rt△ABC中,∠BAC=90°,AB=5,AC=12,将△ABC沿射线BC方向平移m个单位长度到△DEF,顶点A、B、C分别与D、E、F对应,若以点A、D、E为顶点的三角形是等腰三角形,则m的值是 .
科目:初中数学 来源:广州市2018学年度七年级(上)数学期末测试卷 题型:单选题
下列说法正确的是 ( )
A. 两点的所有连线中,直线最短 B. 连接两点之间的线段,叫做这两点之间的距离
C. 锐角的补角一定是钝角 D. 一个角的补角一定大于这个角
C 【解析】试题分析:A、应为两点之间线段最短,故本选项错误; B、应为连接两点间的线段的长度叫两点的距离,故本选项错误; C、锐角的补角一定是钝角,该选项正确; D、钝角的补角小于钝角,故本选项错误. 故选C.查看答案和解析>>
科目:初中数学 来源:甘肃省武威市2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
用火柴棍像如图这样搭三角形:你能找出规律吗?

猜想:搭 n 个三角形需要___________根火柴棍.
2n+1 【解析】试题解析:搭1个三角形需要2×1+1=3根火柴棍; 搭2个三角形需要2×2+1=5根火柴棍; 搭3个三角形需要2×3+1=7根火柴棍; 搭4个三角形需要2×4+1=9根火柴棍; … 依此类推,可以发现,搭几个三角形需要火柴棍的根数就是2与几的乘积加1. 所以,搭n个三角形需要2×n+1=2n+1根火柴棍.查看答案和解析>>
科目:初中数学 来源:甘肃省武威市2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
下面各组数中,相等的一组是( )
A. 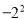 与
与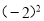 B.
B. 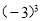 与
与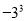 C.
C.  与
与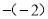 D.
D. 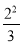 与
与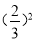
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市2017年中考二模试卷数学试卷 题型:解答题
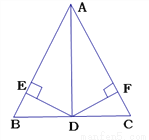
如图,在△ABC中.AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.
(1)求证:AB=AC;
(2)若AD=2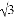 ,∠DAC=30°,求AC的长.
,∠DAC=30°,求AC的长.
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市2017年中考二模试卷数学试卷 题型:填空题
若式子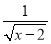 在实数范围内有意义,则x的取值范围是 .
在实数范围内有意义,则x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市2017年中考二模试卷数学试卷 题型:单选题
如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于 AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( )
AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( )
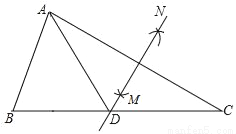
A. 65° B. 60° C. 55° D. 45°
A 【解析】分析:根据线段垂直平分线的性质得到AD=DC,根据等腰三角形的性质得到∠C=∠DAC, 求得∠DAC=30°,根据三角形的内角和得到∠BAC=95°,即可得到结论. 详解:由题意可得:MN是AC的垂直平分线,则AD=DC,故∠C=∠DAC. ∵∠C=30°,∴∠DAC=30°. ∵∠B=55°,∴∠BAC=95°,∴∠BAD=∠BAC﹣∠CAD=65°. ...查看答案和解析>>
科目:初中数学 来源:湖北省襄阳市襄城区2016-2017学年度上学期期末考试八年级数学试卷 题型:填空题
如图,在△ABC中,∠B=63º,∠C=45º,DE⊥AC于E,DF⊥AB于F,那么∠EDF=___________.
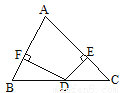
查看答案和解析>>
科目:初中数学 来源:2017年山东省枣庄市中考数学模拟试卷 题型:解答题
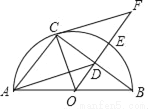
如图,AB是半圆O的直径,E是弧BC的中点,OE交弦BC于点D,点F为OE的延长线上一点且OC2=OD•OF.
(1)求证:CF为⊙O的切线.
(2)已知DE=2,tan∠BAC=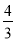 .
.
①求⊙O的半径;
②求sin∠BAD的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com