
����������y��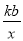 ��ͼ����ͼ��ʾ����һ�κ���y��kx��b(k��0)��ͼ�������( )
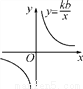
��ͼ����ͼ��ʾ����һ�κ���y��kx��b(k��0)��ͼ�������( )
 ����
����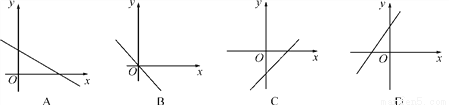
A. A B. B C. C D. D
D ���������������� �ߵ�ͼ����һ�������ޣ���kb��0����k��bͬ�ţ� A��ͼ������������ޣ���k��0��ͼ��y�������ᣬ��b��0����ʱ��k��b��ţ��ʴ�ѡ������⣻ B��ͼ������������ޣ���k��0��ͼ��ԭ�㣬��b=0����ʱ��k��b��ͬ�ţ��ʴ�ѡ������⣻ C��ͼ���һ�������ޣ���k��0��ͼ��y�Ḻ���ᣬ��b��0����ʱ��k��b��ţ��ʴ�ѡ������⣻ ... ���ɶ��ȫ���ƿؾ�ϵ�д�
���ɶ��ȫ���ƿؾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ�����������2016-2017ѧ�����ѧ����ĩ�������꼶��ѧ�Ծ� ���ͣ���ѡ��
�����ϵĵ�A��ԭ��ľ�����3�����A��ʾ����Ϊ�� ��
A. 3��3 B. 6 C. ��6 D. 6��6
A ��������������������������x����|x|=3�����x=+3��3����ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������У2017-2018ѧ����꼶��ѧ�ڵڶ��ο�����ѧ�Ծ� ���ͣ���ѡ��
��ͼ����һ�����������εĵ�������������һ���㣬��Ϊ��һ�㣬�ڶ���ÿ���������㣬���� ��ÿ���������㣬�������ƣ����n�������ε�����ܵ���Ϊ331����n���ڣ� ��
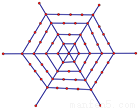
A. n=6 B. n=8 C. n=11 D. n=13
C ���������۲�ͼ�Σ�������ɵã� ��һ��ĵ�ĸ���Ϊ��1���� �ڶ���ĵ�ĸ���Ϊ��6=1��6�������� ������ĵ�ĸ���Ϊ��6+6=2��6�������� ���IJ�ĵ�ĸ���Ϊ��6+6+6=3��6�������� ������ ��n��ĵ�ĸ���Ϊ��(n-1)��6��������������nΪ������ ��ǰn��ĵ���ܸ���Ϊ�� �ɽ�ã��������⣬��ȥ��. ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ�²ᣨ��ʦ��棩�����м���� ���ͣ������
�ⷽ�̣� 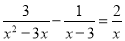 .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ�²ᣨ��ʦ��棩�����м���� ���ͣ������
��ƽ��ֱ������ϵ�У���֪һ�κ���y=x��1��ͼ��P1��x1��y1����P2��x2��y2�����㣬��x1��x2����y1 y2�����������������=����
. �������� �������������k=1���һ�κ��������ʼ��ɵó�y=x��1Ϊ���������������ٸ���x1��x2���ɵó�y1��y2������ý⣮ ��һ�κ���y=x��1��k=1����y��xֵ����������� ��x1��x2����y1��y2���ʴ�Ϊ�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ�²ᣨ��ʦ��棩�����м���� ���ͣ���ѡ��
ij�������ܲ��������ڹ���ij��ͣ����һ��ʱ�䣬����ԭ·���ٲ��лؼң�������ҵľ���y��ʱ��x�Ĺ�ϵ�Ĵ���ͼ���ǣ� ��
A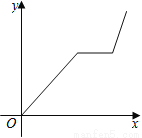 B
B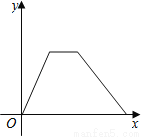 C��
C��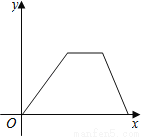 D��
D��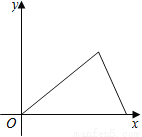
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ���ѧ ��24��С���븴ϰ ���� ���ͣ������
��ͼ��AB�ǡ�O��һ���ң���C�ǡ�O��һ���㣬�ҡ�ACB=30�㣬��E��F�ֱ���AC��BC���е㣬ֱ��EF���O����G��H���㣮����O�İ뾶Ϊ7����GE+FH�����ֵΪ ��
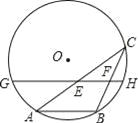
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��ұ�н���ְ�2017-2018ѧ����꼶��ѧ�ڵڶ����¿���12�£���ѧ�Ծ� ���ͣ������
��ͼ��ʾ����ֱ������ABCD�У���ABC=90�㣬AD��BC��AB=BC��E��AB���е㣬CE��BD
��1����֤��BE=AD��
��2����֤��AC���߶�ED�Ĵ�ֱƽ���ߣ�
��3����DBC�ǵ�����������?��˵������
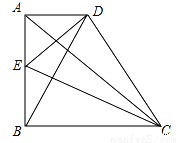
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
��ͼ����֪�߶�a��b��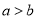 ������һ���߶�AD,ʹ������
������һ���߶�AD,ʹ������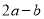 ����ȷ�Ļ����ǣ� ��
����ȷ�Ļ����ǣ� ��
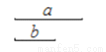
A. 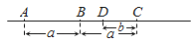 B.
B. 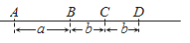
C. 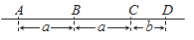 D.
D. 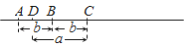
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com