
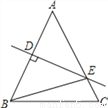
如图,△ABC中,已知BC=12,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长为28,则AC的长为 ______ .
科目:初中数学 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:解答题
在平面直角坐标系xOy中,对称轴为直线x=1的抛物线y=ax2+bx+8过点(﹣2,0).
(1)求抛物线的表达式,并写出其顶点坐标;
(2)现将此抛物线沿y轴方向平移若干个单位,所得抛物线的顶点为D,与y轴的交点为B,与x轴负半轴交于点A,过B作x轴的平行线交所得抛物线于点C,若AC∥BD,试求平移后所得抛物线的表达式.
查看答案和解析>>
科目:初中数学 来源:北京市西城外国语学校2017-2018学年度第一学期八年级数学期中试卷 题型:填空题
若关于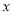 的方程
的方程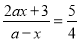 的根为
的根为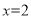 ,则
,则 应取值___.
应取值___.
查看答案和解析>>
科目:初中数学 来源:黑龙江省大庆市2016---2017学年度上期初三数学期末试卷 题型:解答题
列分式方程解应用题:
某学校准备组织部分学生到少年宫参加活动,陈老师从少年宫带回来两条信息:
信息一:按原来报名参加的人数,共需要交费用320元,如果参加的人数能够增加到原来人数的2倍,就可以享受优惠,此时只需交费用480元;
信息二:如果能享受优惠,那么参加活动的每位同学平均分摊的费用比原来少4元.
根据以上信息,原来报名参加的学生有多少人?
20人 【解析】分析:设原来报名参加的学生有x人,根据如果参加的人数能够增加到原来人数的2倍,就可以享受优惠,如果能享受优惠,那么参加活动的每位同学平均分摊的费用比原来少4元,可列方程求解. 本题解析: 【解析】 设原来报名参加的学生有x人, 依题意,得. 解这个方程,得x=20. 经检验,x=20是原方程的解且符合题意. 答:原来报名参加的学生有20人...查看答案和解析>>
科目:初中数学 来源:黑龙江省大庆市2016---2017学年度上期初三数学期末试卷 题型:填空题
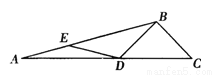
如图,在ΔABC中,∠ABC=120°,点D、E分别在AC和AB上,且AE=ED=DB=BC,则∠A的度数为______°.
查看答案和解析>>
科目:初中数学 来源:黑龙江省大庆市2016---2017学年度上期初三数学期末试卷 题型:单选题
一次智力测验,有20道选择题.评分标准是:对1题给5分,错1题扣2分,不答题不给分也不扣分.小明有两道题未答.至少答对几道题,总分才不会低于60分.则小明至少答对的题数是( )
A.11道 B。12题 C.13题 D.14题
D 【解析】设小明至少答对的题数是x道, 5x-2(20-2-x)≥60, x≥135/7 , 故应为14. 故选D.查看答案和解析>>
科目:初中数学 来源:黑龙江省大庆市2016---2017学年度上期初三数学期末试卷 题型:单选题
如图四个图形中,是中心对称图形的为( )
A.  B.
B.  C.
C.  D.
D. 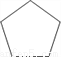
查看答案和解析>>
科目:初中数学 来源:浙江省余姚市2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
如图,在下列条件中,不能证明△ABD≌△ACD的是( )
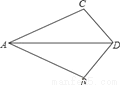
A. BD=DC,AB=AC B. ∠ADB=∠ADC,BD=DC
C. ∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
D 【解析】全等三角形的判定定理有SAS,ASA,AAS,SSS,根据全等三角形的判定定理逐个判断即可. 【解析】 A、∵在△ABD和△ACD中,AD=AD,AB=AC,BD=DC,∴△ABD≌△ACD(SSS),故本选项错误; B、∵在△ABD和△ACD中,BD=DC,∠ADB=∠ADC,AD=AD,∴△ABD≌△ACD(SAS),故本选项错误; C、∵在△ABD和△A...查看答案和解析>>
科目:初中数学 来源:南京市溧水区2016~2017学年度第一学期期末九年级试卷 题型:解答题
关于的一元二次方程x2+2x+k+1=0的有两个实数解是x1和x2.
(1)求k的取值范围;
(2)如果x1+x2-x1x2<-1且k为整数,求k的值.
(1)k≤0;(2)k的值为-1和0. 【解析】试题分析:(1)∵方程有实数根 ∴⊿=22-4k+1)≥0解得 k≤0. (2)根据一元二次方程根与系数的关系,得x1+x2=-2, x1x2=k+1 得 -2—( k+1)<-1 解得 k>-2 ∴ -2<k≤0 ∵k为整数 ∴k的值为-1和0. 试题解析:【解析】 ∵(1)方程有实数根 ∴⊿=22-4k+1)≥0....查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com