练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图所示，两块三角板的直角顶点O重叠在一起，且OB恰好平分∠COD，则∠AOD的度数是____________．

    135． 【解析】本题是有公共定点的两个直角三角形问题，通过图形可知∠AOC+∠BOC=90°，∠BOD+∠BOC=90°，同时∠AOC+∠BOC+∠BOD+∠BOC=180°，可以通过角平分线性质求解． 【解析】 ∵OB平分∠COD， ∴∠COB=∠BOD=45°， ∵∠AOB=90°， ∴∠AOC=45°， ∴∠AOD=135°． 故答案为：135． “点睛”本题...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：浙江省余姚市2017-2018学年七年级上学期期中考试数学试卷 题型：填空题

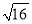    的平方根等于__________.

    ±2 【解析】试题解析：∵=4 4的平方根是±2 ∴的平方根等于±2. 故答案为：±2.

    查看答案和解析>>

    科目：初中数学 来源：云南省2018届九年级上学期期中考试数学试卷 题型：解答题

    如图,将等腰△ABC绕顶点B逆时针方向旋转α度到△A1B1C1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E. F.

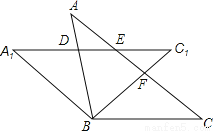
    (1)求证：△BCF≌△BA1D.

    (2)当∠C=α度时,判定四边形A1BCE的形状并说明理由。

    (1)证明见解析(2)四边形A1BCE是菱形 【解析】试题分析：（1）根据等腰三角形的性质得到AB=BC，∠A=∠C，由旋转的性质得到A1B=AB=BC，∠A=∠A1=∠C，∠A1BD=∠CBC1，根据全等三角形的判定定理得到△BCF≌△BA1D；（2）由旋转的性质得到∠A1=∠A，根据平角的定义得到∠DEC=180°﹣α，根据四边形的内角和得到∠ABC=360°﹣∠A1﹣∠C﹣∠A1EC=...

    查看答案和解析>>

    科目：初中数学 来源：云南省2018届九年级上学期期中考试数学试卷 题型：填空题

    已知二次函数的图象开口向下,?且顶点坐标（0，-3）.请写出一个符合条件的二次函数的解析式_____________.

    y=-x2-3 【解析】试题解析：∵若二次函数的图象开口向下，且经过（0，-3）点， ∴y=-x2-3符合要求． 答案不唯一．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年黑龙江省大庆市杜尔伯特县七年级（上）期末数学试卷（五四学制） 题型：解答题

    某校班级篮球联赛中，每场比赛都要分胜负，每队胜1场得3分，负1场得1分，如果某班在第一轮的28场比赛中得48分，那么这个班胜了多少场？

    10场 【解析】试题分析：设这个班胜了x场，则负（28﹣x）场，根据3×胜场数+1×负场数=总分，即可得出关于x的一元一次方程，解之即可得出结论． 试题解析：【解析】 设这个班胜了x场，则负（28﹣x）场，根据题意得： 3x+（28﹣x）=48，解得：x=10． 答：这个班胜了10场．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年黑龙江省大庆市杜尔伯特县七年级（上）期末数学试卷（五四学制） 题型：填空题

    如果收入50元，记作+50元，那么支出30元记作_____元．

    -30 【解析】【解析】 如果收入50元，记作+50元，那么支出30元记作﹣30元，故答案为：﹣30．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年黑龙江省大庆市杜尔伯特县七年级（上）期末数学试卷（五四学制） 题型：单选题

    若关于x的方程mxm－2－m＋3＝0是一元一次方程，则这个方程的解是( )

    A. x＝0 B. x＝3 C. x＝－3 D. x＝2

    A 【解析】试题分析：只含有一个未知数（元），并且未知数的指数是1（次）的方程叫做一元一次方程，它的一般形式是ax+b=0（a，b是常数且a≠0），高于一次的项系数是0． 【解析】 由一元一次方程的特点得m﹣2=1，即m=3， 则这个方程是3x=0， 解得：x=0． 故选：A．

    查看答案和解析>>

    科目：初中数学 来源：上海市长宁区2018届九年级上学期期末质量检测数学试卷 题型：填空题

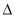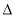    已知ABC与DEF相似，且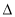ABC与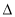DEF的相似比为2:3，若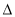DEF 的面积为36，则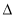ABC的面积等于________．

    16 【解析】∵ABC与DEF相似，且ΔABC与ΔDEF的相似比为2:3， ∴， ∵ΔDEF 的面积为36， ∴ΔABC的面积等于16， 故答案为：16.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学下册（人教版）：期中检测题 题型：解答题

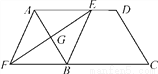
    如图，在平行四边形ABCD中，边AB的垂直平分线交AD于点E，交CB的延长线于点F，连接AF，BE.

    (1)求证：△AGE≌△BGF；

    (2)试判断四边形AFBE的形状，并说明理由．

    (1)证明见解析(2)四边形AFBE是菱形 【解析】试题分析：（1）由平行四边形的性质得出AD∥BC，得出∠AEG=∠BFG，由AAS证明△AGE≌△BGF即可； （2）由全等三角形的性质得出AE=BF，由AD∥BC，证出四边形AFBE是平行四边形，再根据EF⊥AB，即可得出结论． 试题解析：（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠AEG=∠BFG，∵EF垂直...

    查看答案和解析>>

    同步练习册答案