
如果收入50元,记作+50元,那么支出30元记作_____元.
-30 【解析】【解析】 如果收入50元,记作+50元,那么支出30元记作﹣30元,故答案为:﹣30. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:浙江省余姚市2017-2018学年七年级上学期期中考试数学试卷 题型:单选题
有一个两位数,十位数字是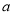 ,个位数字是
,个位数字是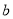 ,若把它们的位置交换,得到新的两位数是( )
,若把它们的位置交换,得到新的两位数是( )
A. 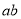 B.
B. 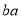 C.
C. 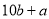 D.
D. 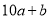
查看答案和解析>>
科目:初中数学 来源:云南省2018届九年级上学期期中考试数学试卷 题型:解答题
解方程:(2x+3)2=2x+3
【解析】试题分析:先移项,再运用因式分解法求解即可. 试题解析:移项, 添括号, 分解因式=0, 化简(2x+3)(2x+2)=0, 即2x+3=0或2x+2=0, ∴ .查看答案和解析>>
科目:初中数学 来源:2017-2018学年黑龙江省大庆市杜尔伯特县七年级(上)期末数学试卷(五四学制) 题型:解答题
如图,C是线段AB上一点,M是AC的中点,N是CB的中点,如果AB=10cm,AC=6cm.
求:(1)AM的长;(2)MN的长.
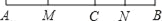
查看答案和解析>>
科目:初中数学 来源:2017-2018学年黑龙江省大庆市杜尔伯特县七年级(上)期末数学试卷(五四学制) 题型:填空题
如图所示,两块三角板的直角顶点O重叠在一起,且OB恰好平分∠COD,则∠AOD的度数是____________.

查看答案和解析>>
科目:初中数学 来源:2017-2018学年黑龙江省大庆市杜尔伯特县七年级(上)期末数学试卷(五四学制) 题型:单选题
如图,AB=12,C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB的长度为( )
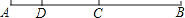
A.4 B.6 C.8 D.10
D. 【解析】 试题分析:∵C为AB的中点,∴AC=BC=AB=×12=6, ∵AD:CB=1:3,∴AD=2, ∴DB=AB-AD=12-2=10(cm). 故选D.查看答案和解析>>
科目:初中数学 来源:上海市长宁区2018届九年级上学期期末质量检测数学试卷 题型:解答题
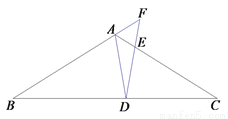
如图,在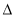 ABC中,点D在边BC上,联结AD,∠ADB=∠CDE,DE交边AC于点E,DE交BA延长线于点F,且
ABC中,点D在边BC上,联结AD,∠ADB=∠CDE,DE交边AC于点E,DE交BA延长线于点F,且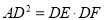 .
.
(1)求证: 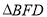 ∽
∽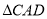 ;
;
(2)求证: 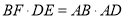 .
.
查看答案和解析>>
科目:初中数学 来源:上海市长宁区2018届九年级上学期期末质量检测数学试卷 题型:单选题
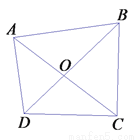
如图,在四边形ABCD中,对角线AC与BD相交于点O,AC平分∠DAB,且∠DAC =∠DBC,那么下列结论不一定正确的是( )
A. 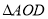 ∽
∽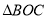 B.
B. 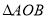 ∽
∽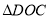 C. CD=BC D.
C. CD=BC D. 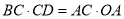
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(人教版):期中检测题 题型:解答题
先化简,再求值: 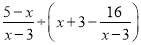 ,其中x=
,其中x=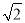 -5.
-5.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com