练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

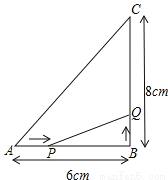
    如图所示，△ABC中，∠B=90°，AB=6cm，BC=8cm．点P从点A开始沿AB边向B以1cm/s的速度移动，点Q从B点开始沿BC边向点C以2cm/s的速度移动．如果P，Q分别从A，B同时出发，

    （1）如果P、Q同时出发，几秒后，可使△PBQ的面积为8平方厘米？

    （2）线段PQ能否将△ABC分成面积相等的两部分？若能，求出运动时间；若不能说明理由．

    （1）2秒或4秒；（2）线段PQ不能否将△ABC分成面积相等的两部分. 【解析】试题分析：（1）设出运动所求的时间，可将BP和BQ的长表示出来，代入三角形面积公式，列出等式，可将时间求出； （2）将△PBQ的面积表示出来，根据△=b2-4ac来判断． 试题解析：（1）设经过x秒，使△PBQ的面积等于8cm2，依题意有： （6-x）•2x=8， 解得x1=2，x2=4，...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省扬州市邗江区2018届九年级（上）期中数学试卷 题型：单选题

    直线l与半径为r的⊙O相交，且点O到直线l的距离为6，则r的取值范围是（　　）

    A. r＜6 B. r=6 C. r＞6 D. r≥6

    C 【解析】【解析】 ∵直线l与半径为r的⊙O相交，且点O到直线l的距离d=6，∴r＞6．故选C．

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省中考数学模拟试卷 题型：解答题

    解方程：y（y﹣4）=﹣1﹣2y．

    【解析】试题分析：因式分解法. 试题解析： 整理得： 解得： 原方程的解是：

    查看答案和解析>>

    科目：初中数学 来源：江西省2017年秋人教七年级数学上册期末模拟卷 题型：单选题

    如图中的图像(折线ABCDE)描述了一汽车在某一直线上的行驶过程中，汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系，根据图中提供的信息，给出下列说法：①汽车共行驶了120千米；②汽车在行驶途中停留了0.5小时；③汽车在整个行驶过程中的平均速度为80.8千米／时；④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减小．⑤汽车离出发地64千米是在汽车出发后1.2小时时。其中正确的说法共有( )

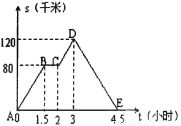
    A.1个 　　　 B．2个 　　　　 C．3个 　　　　 D．4个 

    A. 【解析】 试题分析：根据图象对每条进行分别判断即可，行驶的最远距离是120千米，共行驶240千米，共用时间是4.5小时． ①行驶的最远距离是120千米，共行驶240千米，故此选项错误； ②根据图象从1.5时到2时，是停留时间，停留0.5小时，故此选项正确； ③汽车在整个行驶过程中的平均速度为千米/时，故此选项错误； ④汽车自出发后3小时至4.5小时之间路程...

    查看答案和解析>>

    科目：初中数学 来源：江西省2017年秋人教七年级数学上册期末模拟卷 题型：单选题

    下列美丽的图案中，是轴对称图形的是（ ）

    D 【解析】 试题分析：根据轴对称图形的定义可知：D是轴对称图形，故选：D.

    查看答案和解析>>

    科目：初中数学 来源：河北省2017-2018学年九年级第一学期第一次月考数学试卷 题型：解答题

    已知关于x的一元二次方程x2﹣2mx+(m﹣1)2=0有两个实数根x1，x2．

    （1）求m的取值范围；

    （2）当x12+x22=28时，求m的值．

    （1）m≥；（2）符合条件的m的值为3． 【解析】试题分析：（1）若一元二次方程有两个等实数根，则根的判别式△=b2-4ac≥0，建立关于m的不等式，即可求出m的取值范围； （2）根据根与系数的关系，可得x1+x2=2m，x1·x2=(m﹣1)2，再根据x12+x22=（x1+x2）2-2x1·x2即可求得m的值，结合（1）即可确定出m的具体值. 试题解析：（1）∵原方程有两个实...

    查看答案和解析>>

    科目：初中数学 来源：河北省2017-2018学年九年级第一学期第一次月考数学试卷 题型：单选题

    在解方程（x+2）（x﹣2）=5时，甲同学说：由于5=1×5，可令x+2=1，x﹣2=5，得方程的根x1=﹣1，x2=7；乙同学说：应把方程右边化为0，得x2﹣9=0，再分解因式，即（x+3）（x﹣3）=0，得方程的根x1=﹣3，x2=3．对于甲、乙两名同学的说法，下列判断正确的是..（　　）

    A. 甲错误，乙正确 B. 甲正确，乙错误

    C. 甲、乙都正确 D. 甲、乙都错误

    A 【解析】（x+2）（x﹣2）=5， x2-4=5， x2-9=0， （x+3）（x-3）=0， x+3=0或x-3=0， x1=-3，x2=3， 所以甲错误，乙正确， 故选A.

    查看答案和解析>>

    科目：初中数学 来源：山东省潍坊高新技术产业开发区2017-2018学年八年级上期末模拟数学试卷 题型：解答题

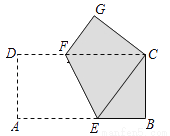
    矩形纸片ABCD的边长AB=4，AD=2．将矩形纸片沿EF折叠，使点A与点C重合，折叠后在其一面着色（如图），则着色部分的面积为多少？

    【解析】试题分析：根据矩形的性质，可得AB与CD的关系，根据翻折的性质，可得∠FEA=∠FEC；AD与CG的关系，根据全等三角形的判定与性质，可得FG与BE的关系，根据勾股定理，可得BE的长，根据面积的和差，可得答案． 试题解析：∵ABCD是矩形， ∴AB||CD， ∴∠FEA=∠EFC， ∵将矩形纸片沿EF折叠，使点A与点C重合，∴∠FEA=∠FEC， ∴∠EFC=∠FE...

    查看答案和解析>>

    科目：初中数学 来源：山东省聊城市莘县2017-2018学年八年级（上）期末模拟数学试卷（含答案） 题型：单选题

    下列说法：①有两条直角边对应相等的两个直角三角形全等；②有斜边对应相等的两个等腰直角三角形全等；③有一条直角边和斜边上的高对应相等的两个直角三角形全等；④有一条边相等的两个等腰直角三角形全等．其中正确的有（　　）

    A. 1个 B. 2个 C. 3个 D. 4个

    C 【解析】因为有两条直角边对应相等的两个直角三角形可利用SAS判定两个直角三角形全等,所以①正确, 因为有斜边对应相等的两个等腰直角三角形可以利用ASA判定两三角形全等,所以②正确,因为有一条直角边和斜边上的高对应相等无法判定两个直角三角形全等,所以③错误,有一条边相等的两个等腰直角三角形可以利用SAS或ASA判定两个直角三角形全等,所以④正确,故选C.

    查看答案和解析>>

    同步练习册答案