
��ͼ����֪������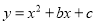 ����A����1��0����B��3��0�����㣮
����A����1��0����B��3��0�����㣮
��1���������ߵĽ���ʽ�Ͷ������ꣻ
��2����0��x��3ʱ����y��ȡֵ��Χ��
��3����PΪ��������һ�㣬��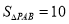 �������ʱ��P�����꣮
�������ʱ��P�����꣮

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017-2018ѧ��ɽ��ʡ����� ���꼶����ĩģ����ѧ�Ծ� ���ͣ������
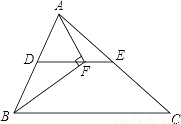
��ͼ���ڡ�ABC��BFƽ�֡�ABC��AF��BF�ڵ�F��DΪAB���е㣬����DF�ӳ���AC�ڵ�E����AB=12��BC=16�����߶�EF�ij�Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ��ׯ��������2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
����A(2,m)��x���ϣ����B(m-1,m+1)�� �� D ��
A. ��һ���� B. �ڶ����� C. �������� D. ��������
D ���������������� �ߵ�A��2��m����x���ϣ� ��m=0�� ���B��m+1��m��1��Ϊ��1����1�����ڵ������ޣ� ��ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����ѧ���꼶�ϲ���ĩ���� ���ͣ���ѡ��
С����ij�̵깺����ƷA,B������,�����ι�����ƷA,B�������ͷ������±�:
������ƷA ������/�� | ������ƷB ������/�� | �����ܷ� ��/Ԫ | |
��һ�ι��� | 4 | 3 | 93 |
�ڶ��ι��� | 6 | 6 | 162 |
��С����Ҫ����3����ƷA��2����ƷB,����Ҫ����(��)
A. 64Ԫ B. 65Ԫ C. 66Ԫ D. 67Ԫ
C ���������������������ƷA�ı��ΪxԪ����ƷB�ı��ΪyԪ�� �������⣬�ã� ��ã� �� ����ƷA�ı��Ϊ12Ԫ����ƷB�ı��Ϊ15Ԫ�� ����3��12+2��15=66Ԫ�� ��ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����ѧ���꼶�ϲ���ĩ���� ���ͣ���ѡ��
�߶�MN��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ,���߶�M1N1��MN����y��Գ�,���M�Ķ�Ӧ��M1������Ϊ(��)
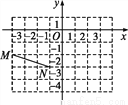
A. (4,2) B. (-4,2) C. (-4,-2) D. (4,-2)
D �������������������ͼ�οɵó���M��-4��-2�������M�Ĺ���y��ԳƵĶ�Ӧ��M1������Ϊ����4��-2���� ��ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶12���¿���ѧ�Ծ� ���ͣ������
��֪����x�ķ���x2����2m+1��x+m��m+1��=0��
��1����֤������������������ȵ�ʵ������
��2���跽�̵������ֱ�Ϊx1��x2����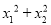 ����Сֵ��
����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶12���¿���ѧ�Ծ� ���ͣ������
��ͼ��ABΪ��O��ֱ������CD��AB��E����֪CD=12��AB=20����OE=_______.
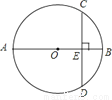
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ�������꼶��̰���ѧ�Ծ���C���� ���ͣ������
ij�̳���������Ϊ30Ԫ/����̨����40Ԫ/�������ۼ��۳���ƽ��ÿ�����۳�600�����г����б�������̨�Ƶ����۵���ÿ����1Ԫʱ�����������ͽ�����10����
��1����ÿ��̨�Ƶ����۵�����40Ԫ/���Ļ������Ǽ�5Ԫ��
���Ǽۺ�ÿ��̨�Ƶ�����Ϊ_______Ԫ��
���Ǽۺ��̳���̨��ƽ��ÿ�µ�������Ϊ_______����
���Ǽۺ��̳�ƽ��ÿ����������___ ____Ԫ��
��2�� ����ÿ��̨�Ƶ����۵�����40Ԫ/���Ļ������Ǽ�aԪ��
�����ú�a�Ĵ���ʽ��գ�
�Ǽۺ�ÿ��̨�Ƶ����ۼ�Ϊ_______Ԫ��
�Ǽۺ�ÿ��̨�Ƶ�����Ϊ_______Ԫ��
�Ǽۺ��̳���̨��ƽ��ÿ�µ�������Ϊ_______����
������̳�Ҫ����������ƽ��ÿ�´ﵽ10000Ԫ���̳�������˵����ԭ�ۼ�ÿ̨40Ԫ�Ļ�����������40Ԫ��������������̳�������˵����������ô�࣬��ԭ�ۼ�ÿ̨40Ԫ�Ļ�����������10Ԫ�Ϳ����ˡ������жϾ��������ҵ�˵���Ƿ���ȷ����˵�����ɣ�
�������� �������������������1�� ��15Ԫ�� ��550���� ��8250Ԫ����2������ƽ��ÿ�����۳�600�������ۼ�ÿ����1Ԫʱ�����������ͽ�����10��֮��Ĺ�ϵ�г�ʽ�ӣ��ٷ�����������ۣ����ÿ�µ����������ٽ��бȽϼ��ɣ� ��������� ��1�� ��15Ԫ�� ��550���� ��8250Ԫ�� ��2�����Ǽۺ�ÿ��̨�Ƶ����ۼ�Ϊ��40+a��Ԫ���Ǽۺ�ÿ��̨�Ƶ�����Ϊ��10+a��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�����������2018����꼶���ϣ�������ѧ�Ծ��������棩 ���ͣ���ѡ��
���г����������¼�Ϊ����¼����ǣ�������
A. ˮ�Ǵ��� B. ������� C. ˮ������ D. Եľ����
B �����������������ˮ�Ǵ����DZ�Ȼ�¼���A����ȷ�� �������������¼���B��ȷ�� ˮ�������Dz������¼���C����ȷ Եľ�����Dz������¼���D����ȷ�� ��ѡB���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com