
��֪����x2k��1 + k = 0�ǹ���x��һԪһ�η��̣��̵Ľ���ڣ� ��
A. ��1 B. 1 C. 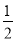 D. ��
D. ��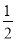

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
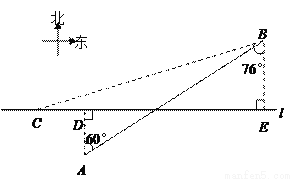
��ͼ���ں���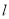 ������ֱ��й۲��A��B����A������
������ֱ��й۲��A��B����A������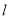 �ľ���Ϊ2km����Bλ�ڵ�A��ƫ��60�㷽������A���10km��������һ���ִ���λ�ڵ�B��ƫ��76�㷽���C�������ظú����������У�5min����ִ�������A�����������D����
�ľ���Ϊ2km����Bλ�ڵ�A��ƫ��60�㷽������A���10km��������һ���ִ���λ�ڵ�B��ƫ��76�㷽���C�������ظú����������У�5min����ִ�������A�����������D����
��1����۲��B������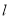 �ľ��룻
�ľ��룻
��2������ִ����е��ٶȣ������ȷ��0.1km/h�������ο����ݣ� 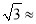 1.73��sin76���0.97��cos��0.24��tan76���0.4.01��
1.73��sin76���0.97��cos��0.24��tan76���0.4.01��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����꼶�²���ѧ ������ ͼ�ε�ƽ������ת ��Ԫ���� ���ͣ���ѡ��
�۲�����ͼ�������м�����Գ�ͼ���������ĶԳ�ͼ�ε��ǣ� ��
A. B.
B. C.
C. D.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶�ϲ���ѧȫ���ۺϲ��Ծ� ���ͣ������
��һЩ��С��ͬ��С�������ɵļ����������ͼ����ͼ����ͼ��ʾ�����ɸü������С�����������______����
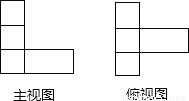
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶�ϲ���ѧȫ���ۺϲ��Ծ� ���ͣ���ѡ��
�ĸ�������a��b��c��d����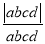 =��1����
=��1����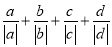 �����ֵΪ��������
�����ֵΪ��������
A. 1 B. 2 C. 3 D. 4
B ���������������� ���ĸ�������a��b��c��d���㣬 ��a��b��c��d�ĸ�������1��������3�������� ��a��b��c��d�ĸ�������1������ʱ�� =1+1+1-1=2�� ��a��b��c��d�ĸ�������3������ʱ�� =-1-1+1-1=-2�� ���ֵ��2����ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶�²���ѧ ������ ���ʳ��� ��Ԫ���� ���ͣ������
������Ϊ50�������ֳ�6�飬���У���1��2��3��4��5���Ƶ��֮����0.96����ô��6���Ƶ����_________ ��
2 �����������������Ƶ���ֲ����У�Ƶ��֮�͵���1�����6���Ƶ��Ϊ��1-0.96=0.04��Ƶ��=����������Ƶ��=50��0.04=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶�²���ѧ ������ ���ʳ��� ��Ԫ���� ���ͣ������
��50�����ݣ����ֳ�6�飬��1��4���Ƶ���ֱ�Ϊ10��8��7��11����5���Ƶ����0.16�����6���Ƶ����__________��
6�� ��������������������ȸ���Ƶ��=Ƶ��������������õ�5���Ƶ����Ȼ�����6�����Ƶ���͵�����������������õ�6���Ƶ��������50�����ݣ����ֳ�6�飬��5���Ƶ����0.16�����5���Ƶ��Ϊ50��0.16=8���֡ߵ�1��4���Ƶ���ֱ�Ϊ10��8��7��11�����6���Ƶ��Ϊ50����10+8+7+11+8��=6���ʴ�Ϊ��6���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ��ʦ����ϲ� ��4�� ͼ�ε����� ��Ԫ���Ծ� ���ͣ������
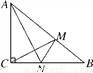
��ͼ����Rt��ABC�У���ACB��90�㣬AC��6cm��BC��8cm.����M�ӵ�B��������BA������ÿ��3cm���ٶ���A�˶���ͬʱ����N�ӵ�C��������CB������ÿ��2cm���ٶ����B�˶����˶�ʱ��Ϊt��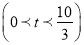 ������MN.
������MN.
(1)����BMN���ABC���ƣ���t��ֵ��
(2)����AN��CM����AN��CM����t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�˽̰����꼶��ѧ�²���ϰ����ʮ�´����� ���ͣ���ѡ��
ijУѧ�����Լס��ҡ���������������������Ϊ2��3��5����ͼ��ʾ������ͼ��ʾ�����ֲ��������֪���Լ�����Ϊ180�ˣ�������˵������ȷ���� (����)
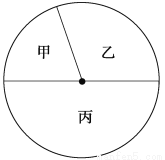
A�����μ�Բ�Ľ���72��
B��ѧ������������900��
C�����������������ҵ�����������180��
D�������������ȱ�������������180��
D ������������֪�ã����μ�Բ�Ľ��ǡ�360�㣽72�㣬Aѡ����ȷ��ѧ������������180�£�900��Bѡ����ȷ���ҵ���������900����270����������������900����450������Cѡ����ȷ����ѡD.�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com