
如图,在4×4正方形网格中,黑色部分的图形构成一个轴对称图形,现在任选取一个白色的小正方形并涂黑,使图中黑色部分的图形仍然构成一个轴对称图形的概率是______.

 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源:山西省2017-2018学年八年级上期末模拟数学试卷 题型:单选题
已知9x2+kxy+4y2是一个完全平方展开式,那么k的值是( )
A. 12 B. 24 C. ±12 D. ±24
C 【解析】已知9x2+kxy+4y2是一个完全平方展开式,中间一项为加上或减去3x和2y积的2倍,所以k=±12.故选C.查看答案和解析>>
科目:初中数学 来源:黑龙江省密山市2017-2018学年八年级上学期期中考试数学试卷 题型:填空题
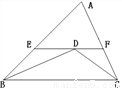
如图,△ABC中,∠ABC与∠ACB的平分线相交于点D,过点D作直线EF‖BC,交AB于点E、交AC于点F若BE=4,EF=7,则FC=____。
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷(C卷) 题型:解答题
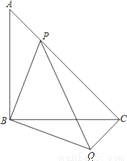
如图,等腰直角△ABC中,∠ABC=90°,点P在AC上,将△ABP绕顶点B沿顺时针方向旋转90°后得到△CBQ.
(1)求∠PCQ的度数;
(2)当AB=4,AP:BP=1:3时,求PQ的长;
(3)当点P在线段AC上运动时(P不与A、C重合),请写出一个反映PA2、PC2、PB2之间关系的等式,并加以证明.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷(C卷) 题型:填空题
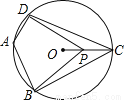
如图,四边形ABCD内接于⊙O,∠DAB=120°,连接OC,点P是半径OC上任意一点,连接DP,BP,则∠BPD可能为______度(写出一个即可).
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷(C卷) 题型:单选题
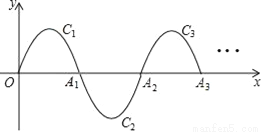
如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,得到Cn,若点P(2017,m)在抛物线Cn上,则m为( )
A. 1 B. ﹣1 C. 2 D. ﹣2
A 【解析】∵一段抛物线:y=-x(x-2)(0≤x≤2), ∴图象与x轴交点坐标为:(0,0),(2,0), ∵将C1绕点A1旋转180°得C2,交x轴于点A2; 将C2绕点A2旋转180°得C3,交x轴于点A3; … 如此进行下去,直至得Cn. ∵2017÷2=1008……1, ∴点P(2017,m)在C1009上, ∴C1009的与x轴的...查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷(C卷) 题型:单选题
设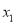 、
、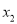 是一元二次方程
是一元二次方程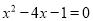 的两个根,则
的两个根,则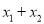 的值为( ).
的值为( ).
A. 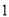 B.
B. 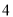 C.
C. 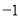 D.
D. 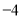
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷(A卷) 题型:填空题
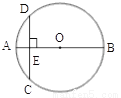
如图,AB是⊙O的直径,CD为⊙O的一条弦,且CD⊥AB于点E,已知CD=4,AE=1,则⊙O的半径为_________.
查看答案和解析>>
科目:初中数学 来源:广西南宁市2017年中考数学一模试卷 题型:解答题
如图,在网格中建立了平面直角坐标系,每个小正方形的边长均为1个单位长度,将四边形ABCD绕坐标原点顺时针方向旋转180°后得到四边形A1B1C1D1 .
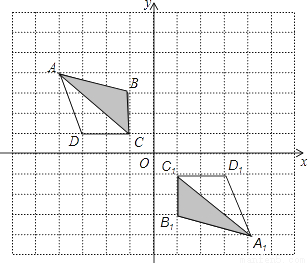
(1)写出点D1的坐标________;
(2)将四边形A1B1C1D1平移,得到四边形A2B2C2D2,若点D2(4,5),画出平移后的图形;
(3)求点D旋转到点D1所经过的路线长.
(1)(3,﹣1);(2)作图见解析;(3) . 【解析】试题分析:(1)利用第四象限点的坐标特征写出点D1的坐标; (2)利用点D1与D2的坐标变化规律得到将四边形A1B1C1D1平移先向上平移6个单位,再向右平移1个单位得到四边形A2B2C2D2,然后利用平移规律画图; (3)先利用勾股定理计算OD,然后根据弧长公式计算点D旋转到点D1所经过的路线长. 试题解析:(1)...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com