练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

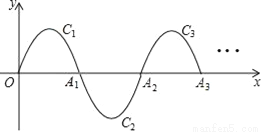
    如图，一段抛物线：y=﹣x（x﹣2）（0≤x≤2）记为C1，它与x轴交于两点O，A1；将C1绕A1旋转180°得到C2，交x轴于A2；将C2绕A2旋转180°得到C3，交x轴于A3；…如此进行下去，得到Cn，若点P（2017，m）在抛物线Cn上，则m为（ ）

    A. 1 B. ﹣1 C. 2 D. ﹣2

    A 【解析】∵一段抛物线：y=-x（x-2）（0≤x≤2）， ∴图象与x轴交点坐标为：（0，0），（2，0）， ∵将C1绕点A1旋转180°得C2，交x轴于点A2； 将C2绕点A2旋转180°得C3，交x轴于点A3； … 如此进行下去，直至得Cn． ∵2017÷2=1008……1， ∴点P（2017，m）在C1009上， ∴C1009的与x轴的...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2016-2017学年黑龙江省哈尔滨市松北区2017届九年级上学期期末数学试卷 题型：解答题

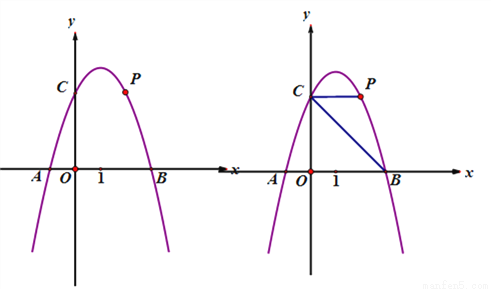
    如图，抛物线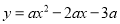交X轴于点A、B（A左B右），交Y轴于点C，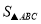

    =6，点P为第一象限内抛物线上的一点.

    （1）求抛物线的解析式；

    （2）若∠PCB=45°，求点P的坐标；

    （3）点Q为第四象限内抛物线上一点，点Q的横坐标比点P的横坐标大1，连接PC、

    AQ，当PC=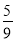AQ时，求点P的坐标以及ΔPCQ的面积.

    （1）y=?x²+2x+3；（2）P(2,3)；（3）P(,)， . 【解析】试题分析：（1）根据抛物线的解析式求得点A、B、C的坐标，根据， =6即可求得a值，从而求得抛物线的解析式；（2）根据点B、C的坐标判定△OBC是等腰直角三角形，即可得∠BCO=∠OBC=45°，已知点P为第一象限内抛物线上的一点,且∠PCB=45°，可得PC∥OB，所以P点的纵坐标为3，令y=3，解方程即可求得点...

    查看答案和解析>>

    科目：初中数学 来源：黑龙江省密山市2017-2018学年八年级上学期期中考试数学试卷 题型：解答题

    如图，x轴、y轴上两点坐标分别是A(0,4)B(3,0)，若在x轴上找一点C，使△ABC为等腰三角形，则满足条件的点C有（ ）。

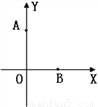
    A. 2个 B. 3个 C. 4个 D. 5个

    C 【解析】①若AP=AB，以A为圆心，AB为半径画弧与x轴有1个交点（A点除外），即满足△ABP是等腰三角形的P点有1个；②若BP=AB，以B为圆心，BA为半径画弧与x轴有2个交点，即满足△ABP是等腰三角形的P点有2个；③若PA=PB，作AB的垂直平分线与x轴只有一个交点，即满足△ABP是等腰三角形的P点有1个；所以点P在x轴上，△ABP是等腰三角形，符合条件的点P共有4个．故选C.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷（C卷） 题型：解答题

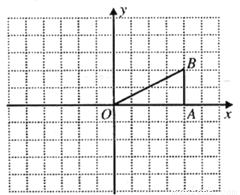
    在下图的正方形网格中有一个三角形OAB，请你在网格中按要求画出图形：

    （1）画出△OAB向左平移3个单位后的三角形；

    （2）画出△OAB绕点O旋转180°后的三角形；

    （3）画出△OAB沿OA翻折后的图形．

    答案见解析． 【解析】试题分析：（1）把每一个点都移动三个单位得到A1B1C1，连接A1B1C1.(2)作B,A点关于原点的对称点B2,A2,连接A2B2O.(3)作B点关于x轴的对称点B3,连接AB3O. 试题解析： 【解析】 （1）如图所示：△A1B1C1即为所求. （2）如图所示：△A2B2O即为所求. （3）如图所示：△AB3O即为所求.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷（C卷） 题型：填空题

    如图，在4×4正方形网格中，黑色部分的图形构成一个轴对称图形，现在任选取一个白色的小正方形并涂黑，使图中黑色部分的图形仍然构成一个轴对称图形的概率是______．

    【解析】 如图，有5种不同取法；故概率为 .

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷（C卷） 题型：单选题

    在一个不透明的布袋中，红色、黑色、白色的球共有20个，除颜色外，形状、大小、质地等完全相同，小明通过大量摸球实验后发现摸到红色、黑色球的频率分别稳定在10%和30%，则口袋中白色球的个数很可能是( )个．

    A. 10 B. 11 C. 12 D. 13

    C 【解析】由题意可得：白色球的个数可能为： （个）. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷（A卷） 题型：解答题

    已知：关于x的一元二次方程x2﹣6x﹣m=0有两个实数根．

    （1）求m的取值范围；

    （2）如果m取符合条件的最小整数，且一元二次方程x2﹣6x﹣m=0与x2+nx+1=0有一个相同的根，求常数n的值．

    （1）m≥﹣9；（2 ）. 【解析】试题分析：（1）根据判别式的意义得到△=（﹣6）2﹣4×1×（﹣m）≥0，然后解不等式即可得到m的范围； （2）在（1）中m的取值范围内确定满足条件的m的值，再解方程x2﹣6x﹣m=0，然后把它的解代入x2+nx+1=0可计算出n的值． 试题解析：【解析】 （1）根据题意得△=（﹣6）2﹣4×1×（﹣m）≥0，解得m≥﹣9； （2）∵m...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷（A卷） 题型：单选题

    如图，A、B、C是⊙O上的三点，∠BOC=70°，则∠A的度数为（　　）

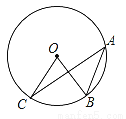
    A. 70° B. 45° C. 40° D. 35°

    D 【解析】∠A=∠BOC=35°. 故选D.

    查看答案和解析>>

    科目：初中数学 来源：广西南宁市2017年中考数学一模试卷 题型：填空题

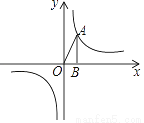
    如图，点A为反比例函数y=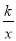图象上的一点，过点作AB⊥x轴于点B，连接OA，若△OAB的面积为4，则k=________．

    8 【解析】试题解析：由题意得： |k|=4，解得k=±8． ∵反例函数图象位于一三象限， ∴k＞0， ∴k=8． 故答案为8．

    查看答案和解析>>

    同步练习册答案