
���������У����ξ��ж����β�һ�����е��ǣ�������
A. �Խ������ B. �Խ�����ƽ��
C. �Խ����ഹֱ D. �ڱ����
A �����������ε������У��ı�����ȣ�����Ա߷ֱ�ƽ�У��Խ���ȣ��ڽǻ������Խ����ഹֱ��ƽ�֣���ÿһ��Խ���ƽ��һ��Խǣ� ���ε������У�����Ա߷ֱ���ȣ�����Ա߷ֱ�ƽ�У��ĸ��ڽǶ���ֱ�ǣ��Խ��������ƽ�֣� ����ξ��ж����β�һ�����е������ǶԽ�����ȣ� ��ѡA�� Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д� �����ҵ��ٿ���������������ϵ�д�
�����ҵ��ٿ���������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶���ϣ�������ѧ�Ծ� ���ͣ������
��֪��ƽ���ı���ABCD������AB��AD�ij��ǹ���x�ķ���x2��mx+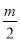 -
-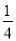 =0������ʵ������
=0������ʵ������
��1��mΪ��ֵʱ���ı���ABCD�����Σ������ʱ���εı߳���
��2����AB�ij�Ϊ2����ôƽ���ı���ABCD���ܳ��Ƕ��٣�
��1��m=1ʱ���ı���ABCD�����Σ�����ABCD�ı߳��ǣ���2��ƽ���ı���ABCD���ܳ���5�� ����������������� ��1�����ı���ABCD�����Σ� ��AB=AD�� ���=0����m2��4������=0�� �����ã���m��1��2=0�� ���m=1�� ��m=1ʱ��ԭ����Ϊx2��x+=0�� ��ã�x1=x2=0.5�� �ʵ�m=1ʱ���ı���ABCD�����Σ����εı�...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�����ɹŰ�ͷ�����꼶���£�������ѧ�Ծ� ���ͣ���ѡ��
��֪x+y=��5��xy=3����x2+y2=��������
A. 25 B. ��25 C. 19 D. ��19
C ���������������� ��x+y=��5��xy=3����x2+y2=��x+y��2��2xy=25��6=19����ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ������������2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
��ͼ��ֱ��l1��l2��l3��һ����ֱ��������ABC����������A��B��C�ֱ���l1��l2��l3�ϣ�AC��l2��D����ACB=90�㣮��֪l1��l2�ľ���Ϊ2��l2��l3�ľ���Ϊ6����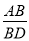 ��ֵΪ_____��
��ֵΪ_____��
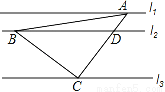
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ������������2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ���ѡ��
ij��Ʒ���˶����������ν��ۣ�ÿ�����ۼ���560Ԫ��Ϊ315Ԫ����֪���ν��۵İٷ�����ͬ����ÿ�ν��۵İٷ��ʣ���ÿ�ν��۵İٷ���Ϊx���������еķ�������ȷ���ǣ�������
A. 560��1��x��2��315 B. 560��1��x��2��315
C. 560��1��2x��2��315 D. 560��1��x2����315
B ������������������������⣬����ÿ�ν��۵İٷ���Ϊx�����з���Ϊ560��1-x��²=315. ��ѡ��B�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�����ɹŰ�ͷ�а��꼶���£�������ѧ�Ծ� ���ͣ������
��ͼ����ABC�͡�ADE���ǵ���ֱ�������Σ�CE��BD�ཻ�ڵ�M��BD��AC�ڵ�N��֤����
��1����ABD�ա�ACE
��2��BD��CE��
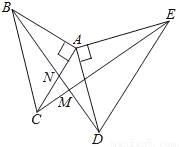
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�����ɹŰ�ͷ�а��꼶���£�������ѧ�Ծ� ���ͣ������
��ͼ���ڡ�ABC�У�AB=AC��AD=BD=BC����ô��A=__�ȣ�
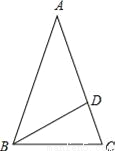
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������Դ��2016-2017ѧ���һѧ����ĩ���Ծ��꼶��ѧ�Ծ� ���ͣ������
��ͼ��������y=��x2��2x+3��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ߣ�����y�ύ�ڵ�C����DΪ�����ߵĶ��㣮
��1�����A��B��C�����ꣻ
��2����M��m��0��Ϊ�߶�AB��һ�㣨��M�����A��B�غϣ�������M��x��Ĵ��ߣ���ֱ��AC���ڵ�E���������߽��ڵ�P������P��PQ��AB���������ڵ�Q������Q��QN��x���ڵ�N���ɵþ���PQNM����ͼ����P�ڵ�Q��ߣ����ú�m��ʽ�ӱ�ʾ����PQNM���ܳ���
��3��������PQNM���ܳ����ʱ��m��ֵ�Ƕ��٣��������ʱ�ġ�AEM�������
��4���ڣ�3���������£�������PMNQ���ܳ����ʱ������DQ������������һ��F��y���ƽ���ߣ���ֱ��AC���ڵ�G����G�ڵ�F���Ϸ�������FG=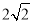 DQ�����F�����꣮
DQ�����F�����꣮
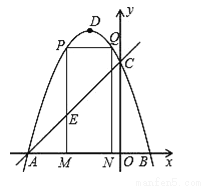
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ���Ƹ��й�����2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
������x��һԪ���η���x2 ��4x +m = 0��������ȵ�ʵ��������m =______��
4 ����������һԪ���η���x2 ��4x +m = 0��������ȵ�ʵ������ ���=(-4)2-4m=0, ��4m=16, ��m=4.�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com