
科目:初中数学 来源:山东省临朐县沂山风景区2018届九年级上期末模拟数学试卷 题型:解答题
如图,已知反比例函数y1=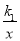 (k1>0)与一次函数y2=k2x+1(k2≠0)相交于A、B两点,AC⊥x轴于点C.若△OAC的面积为1,且tan∠AOC=2.
(k1>0)与一次函数y2=k2x+1(k2≠0)相交于A、B两点,AC⊥x轴于点C.若△OAC的面积为1,且tan∠AOC=2.
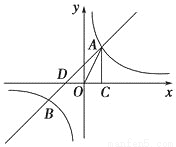
(1)求出反比例函数与一次函数的解析式;
(2)请直接写出B点的坐标,并指出当x为何值时,反比例函数y1的值大于一次函数y2的值?
(1)反比例函数的表达式为y1=,一次函数的表达式y2=x+1;(2)当0<x<1或x<-2时,y1>y2. 【解析】试题分析:(1)、首先设OC=m,根据tan∠AOC的大小求出AC的值,然后根据三角形的面积得出m的值,从而得到点A的坐标,然后求出函数解析式;(2)、根据图象得出答案. 试题解析:(1)、在Rt△OAC中,设OC=m,∵tan∠AOC==2,∴AC=2×OC=2m, ...查看答案和解析>>
科目:初中数学 来源:浙江省宁波市东钱湖九校2018届九年级上册期中联考数学试卷 题型:单选题
某学校在进行防溺水安全教育活动中,将以下几种在游泳时的注意事项写在纸条上并折好,内容分别是:①互相关心;②互相提醒;③不要相互嬉水;④相互比潜水深度;⑤选择水流湍急的水域;⑥选择有人看护的游泳池.小颖从这6张纸条中随机抽出一张,抽到内容描述正确的纸条的概率是( )
A. 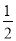 B.
B. 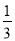 C.
C. 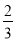 D.
D. 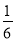
查看答案和解析>>
科目:初中数学 来源:安徽省宿州市(城西校区) 2017-2018学年九年级第一学期期中测试数学试卷 题型:单选题
如图,已知四边形ABCD是平行四边形,下列结论中错误的是( )
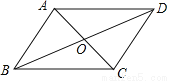
A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
D 【解析】试题分析:A、根据邻边相等的平行四边形是菱形可知四边形ABCD是菱形,故本选项不符合题意; B、根据对角线垂直的平行四边形是菱形可知四边形ABCD是菱形,故本选项不符合题意; C、根据有一个角是直角的平行四边形是矩形可知四边形ABCD是矩形,故本选项不符合题意; D、根据对角线相等的平行四边形是矩形可知四边形ABCD是矩形,但不一定是正方形,故本选项符合题意. ...查看答案和解析>>
科目:初中数学 来源:2017年安徽省中考数学三模试卷 题型:解答题
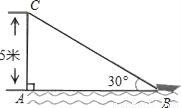
如图,在离水面高度为5m的岸上有人用绳子拉船靠岸,开始绳子与水面的夹角为30°,此人以每秒0.5m的速度收绳.
(1)8秒后船向岸边移动了多少米?
(2)写出还没收的绳子的长度S米与收绳时间t秒的函数关系式.
查看答案和解析>>
科目:初中数学 来源:2017年安徽省中考数学三模试卷 题型:单选题
根据关于x的一元二次方程x2+px+q=0,可列表如下:则方程x2+px+q=0的正数解满足( )
x | 0 | 0.5 | 1 | 1.1 | 1.2 | 1.3 |
x2+px+q | ﹣15 | ﹣8.75 | ﹣2 | ﹣0.59 | 0.84 | 2.29 |
A. 解的整数部分是0,十分位是5 B. 解的整数部分是0,十分位是8
C. 解的整数部分是1,十分位是1 D. 解的整数部分是1,十分位是2
C 【解析】根据表中函数的增减性,可以确定函数值是0时,x应该是大于1.1而小于1.2. 所以解的整数部分是1,十分位是1. 故选:C.查看答案和解析>>
科目:初中数学 来源:2017年安徽省中考数学三模试卷 题型:单选题
如图,下列条件中,能判断直线l1∥l2的是( )
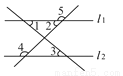
A. ∠2=∠3 B. ∠1=∠3 C. ∠4+∠5=180° D. ∠2=∠4
B 【解析】A、∠2和∠3不是直线l1、l2被第三条直线所截形成的角,故不能判断直线l1∥l2. B、∵∠1=∠3,∴l1∥l2(同位角相等两直线平行). C、∠4、∠5是直线l1、l2被第三条直线所截形成的同位角,故∠4+∠5=180°不能判断直线l1∥l2. D、∠2、∠4是直线l1、l2被第三条直线所截形成的同旁内角,故∠2=∠4不能判断直线l1∥l2. 故选B...查看答案和解析>>
科目:初中数学 来源:2017-2018学年北师大版八年级数学下册 期末测评 题型:单选题
如图所示,在?ABCD中,分别以AB,AD为边向外作等边△ABE,△ADF,延长CB交AE于点G,点G在点A,E之间,连接CG,CF,则下列结论不一定正确的是( )
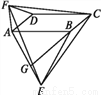
A. △CDF≌△EBC
B. ∠CDF=∠EAF
C. CG⊥AE
D. △ECF是等边三角形
C 【解析】A.在平行四边形ABCD中,∠ADC=∠ABC,AD=BC,CD=AB, ∵△ABE、△ADF都是等边三角形, ∴AD=DF,AB=EB,∠ADF=∠ABE=60°, ∴DF=BC,CD=BC, ∴∠CDF=360°-∠ADC-60°=300°-∠ADC, ∠EBC=360°-∠ABC-60°=300°-∠ABC, ∴∠CDF=∠EBC, ...查看答案和解析>>
科目:初中数学 来源:浙江省宁波市东海实验学校2017年中考数学模拟试卷 题型:填空题
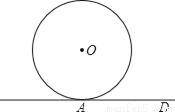
如图,杭州乐园的摩天轮半径为25米,已知摩天轮绕圆心O顺时针做匀速运动,旋转一周需12分钟,某人从摩天轮的最低处(地面A处)出发,问经过4分钟后,此人距地面AD的高度是 米.(摩天轮最低处距地面的高度忽略不计)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com