
某学校在进行防溺水安全教育活动中,将以下几种在游泳时的注意事项写在纸条上并折好,内容分别是:①互相关心;②互相提醒;③不要相互嬉水;④相互比潜水深度;⑤选择水流湍急的水域;⑥选择有人看护的游泳池.小颖从这6张纸条中随机抽出一张,抽到内容描述正确的纸条的概率是( )
A. 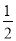 B.
B. 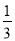 C.
C. 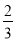 D.
D. 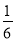
科目:初中数学 来源:湖北省武汉市江夏区2018届九年级上期末模拟数学试卷 题型:填空题
在分别写有﹣1,0,1,2的四张卡片中随机抽取一张,所抽取的数字平方后等于1的概率为 ________.
【解析】试题解析:因为-1,0,1,2的四张卡片中随机抽取一张,所抽取的数字平方后等于1共有2张, 所以所抽取的数字平方后等于1的概率为,查看答案和解析>>
科目:初中数学 来源:山东省临朐县沂山风景区2018届九年级上期末模拟数学试卷 题型:单选题
如图,矩形纸片ABCD中,AB=4,BC=8,将纸片折叠,使点C与点A重合,折痕为EF,点D的对应点为G,连接DG,则图中阴影部分面积是( )
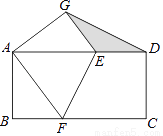
A. 5 B. 3 C. 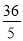 D.
D. 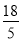
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市东钱湖九校2018届九年级上册期中联考数学试卷 题型:填空题
在一个不透明的口袋中,装有若干个除颜色不同外,其余都相同的小球.如果口袋中装有3个红球且从中随机摸出一个球是红球的概率为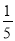 ,那么口袋中小球共有_____个.
,那么口袋中小球共有_____个.
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市东钱湖九校2018届九年级上册期中联考数学试卷 题型:单选题
如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )
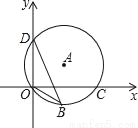
A. 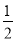 B.
B. 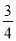 C.
C. 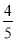 D.
D. 
查看答案和解析>>
科目:初中数学 来源:安徽省宿州市(城西校区) 2017-2018学年九年级第一学期期中测试数学试卷 题型:解答题
用适当的方法解下列方程.
(1).x2-2x=2x+1;
(2).(x+3)2=(1-2x)2.
(1)x1=2+,x2=2-(2)x1=-,x2=4 【解析】试题分析:(1)把含有未知数的项移至方程左边,合并同类项后把等号左边配成完全平方式,然后开方即可; (2)把等号右边的项移至等号左边,然后利用平方差公式分解因式,利用因式分解法求解即可. 试题解析: (1)(配方法)原方程可化为x2-4x=1, 配方,得x2-4x+4=1+4,(x-2)2=5. 两边...查看答案和解析>>
科目:初中数学 来源:安徽省宿州市(城西校区) 2017-2018学年九年级第一学期期中测试数学试卷 题型:单选题
下列说法正确的是( )
A. 对应边都成比例的多边形相似 B. 对应角都相等的多边形相似
C. 边数相同的正多边形相似 D. 矩形都相似
C 【解析】试题分析:根据相似图形的定义,对选项一一分析,排除错误答案. 【解析】 A、对应边都成比例的多边形,属于形状不唯一确定的图形,故错误; B、对应角都相等的多边形,属于形状不唯一确定的图形,故错误; C、边数相同的正多边形,形状相同,但大小不一定相同,故正确; D、矩形属于形状不唯一确定的图形,故错误. 故选C.查看答案和解析>>
科目:初中数学 来源:2017年安徽省中考数学三模试卷 题型:解答题
计算: 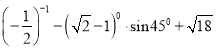 .
.
查看答案和解析>>
科目:初中数学 来源:辽宁省2018届九年级上学期期末考试数学试卷 题型:解答题
随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了个圆形喷水池,在水池中心竖直安装了一根高为2米的喷水管,它喷出的抛物线形水柱在与水池中心的水平距离为1米处达到最高,水柱落地处离池中心3米.
(1)请你建立适当的平面直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度的多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com